Объемная плотность энергии электростатического поля шара. Энергия зарядов, проводников, конденсатора и электростатического поля. Объемная плотность энергии
14.1. Энергия системы точечных зарядов
Рис. 14.1
Из сопоставления (14.1) и (14.2) видно, что Q 1 Q 2 , поэтому энергию системы из двух точечных зарядов можно представить в симметричном виде:
где i – потенциал поля, создаваемого всеми зарядами, кроме i -го, в точке, где расположен i -ый заряд.
^
14.2. Энергия заряженного проводника
Заряд, расположенный на поверхности проводника, можно рассматривать как систему точечных зарядов, поэтому для вычисления энергии заряженного проводника можно воспользоваться формулой (14.4). Потенциал любой точки поверхности проводника одинаков ( i =), поскольку его поверхность эквипотенциальна. Следовательно, в формуле (14.4) потенциал можно вынести за знак суммы:
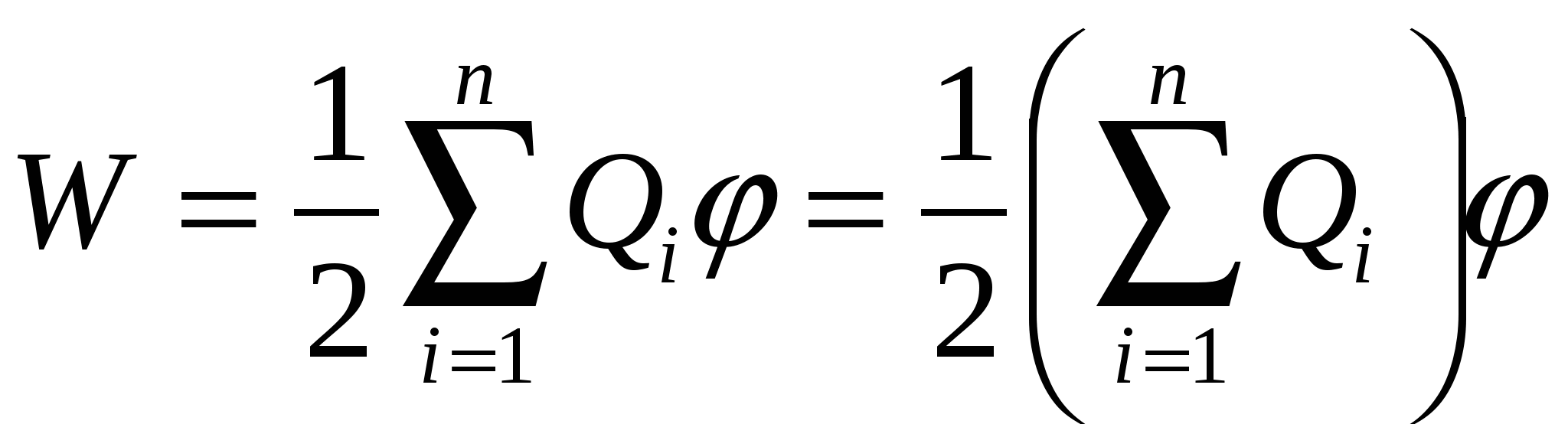 или
или  , (14.5) где
, (14.5) где 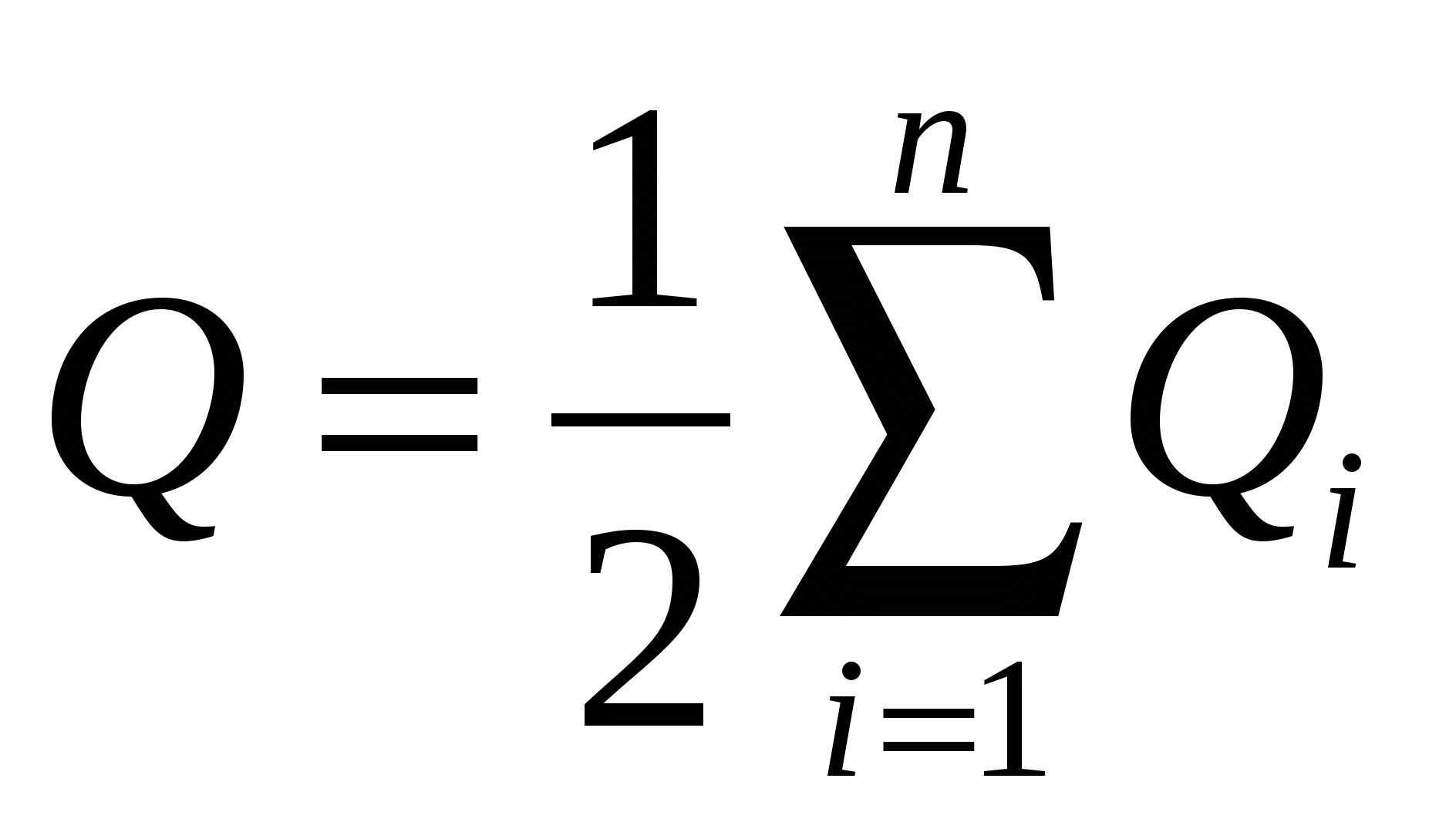 – заряд проводника.
– заряд проводника.
С учётом (13.3) выражение для энергии заряженного проводника можно представить в виде
^
14.3. Энергия заряженного конденсатора. Плотность энергии электростатического поля
Для вычисления энергии заряженного конденсатора воспользуемся формулами (14.5) – (14.7), заменив на разность потенциалов между обкладками конденсатора U=
. Тогда
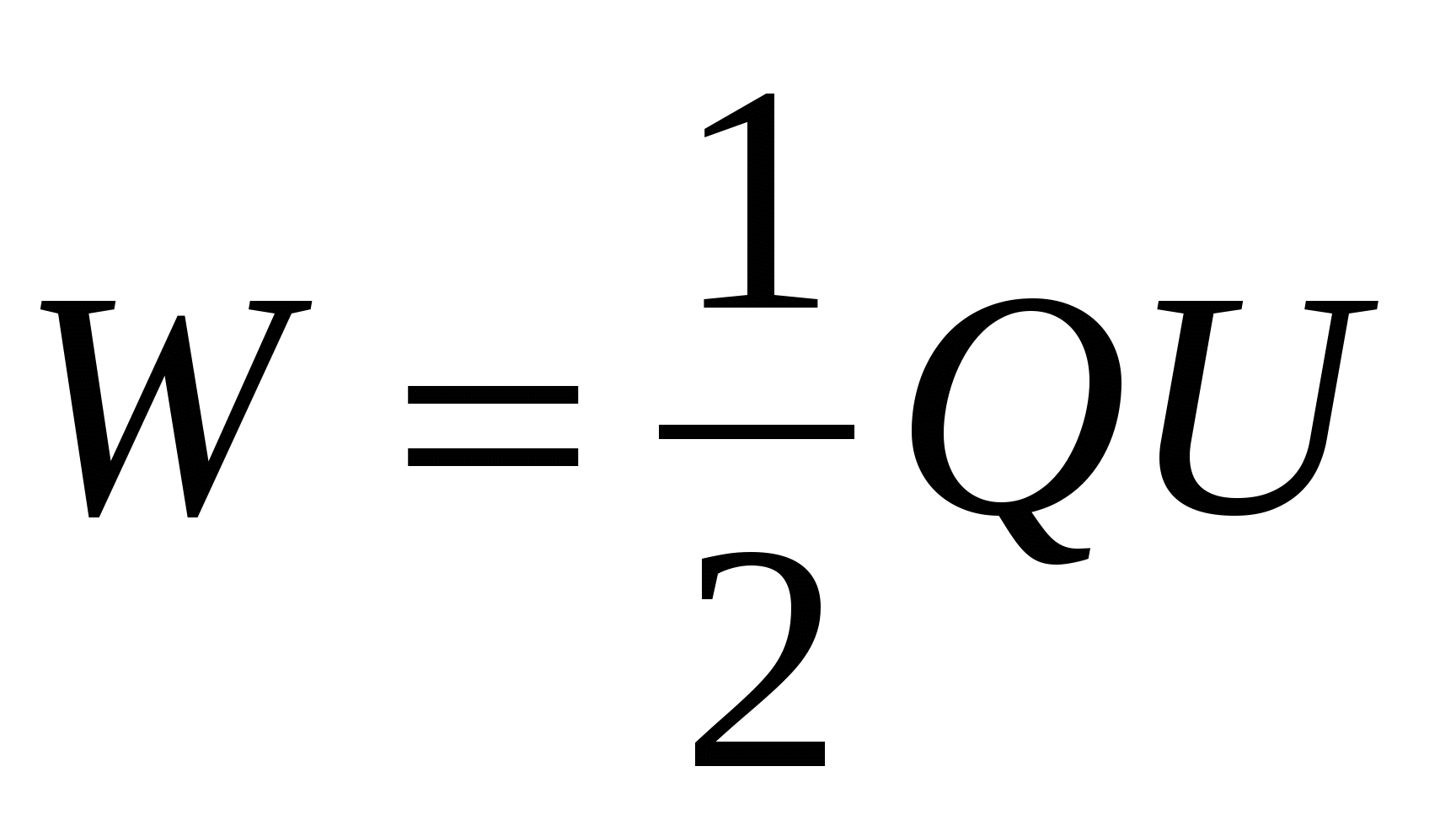 , , | (14.8) |
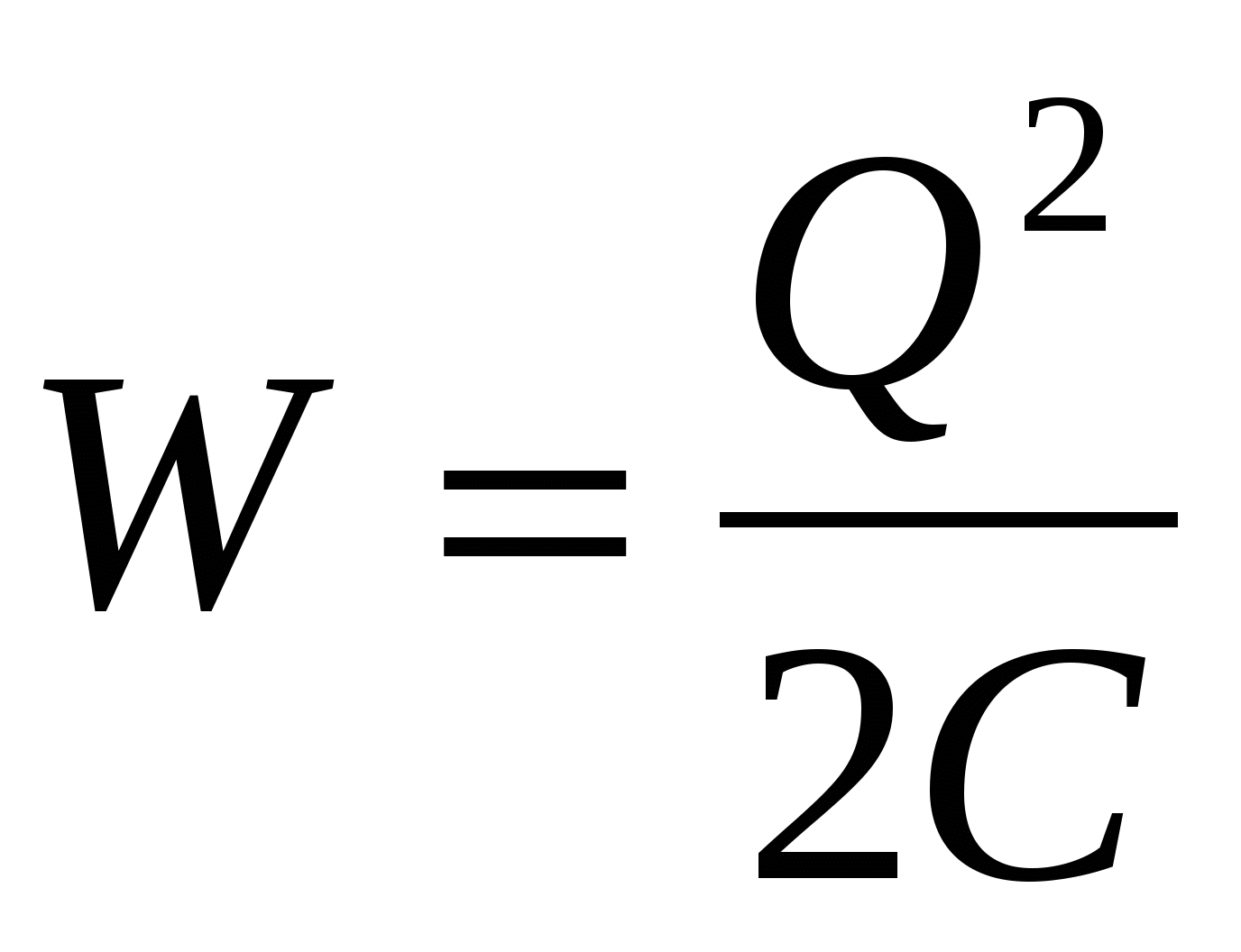 | (14.9) |
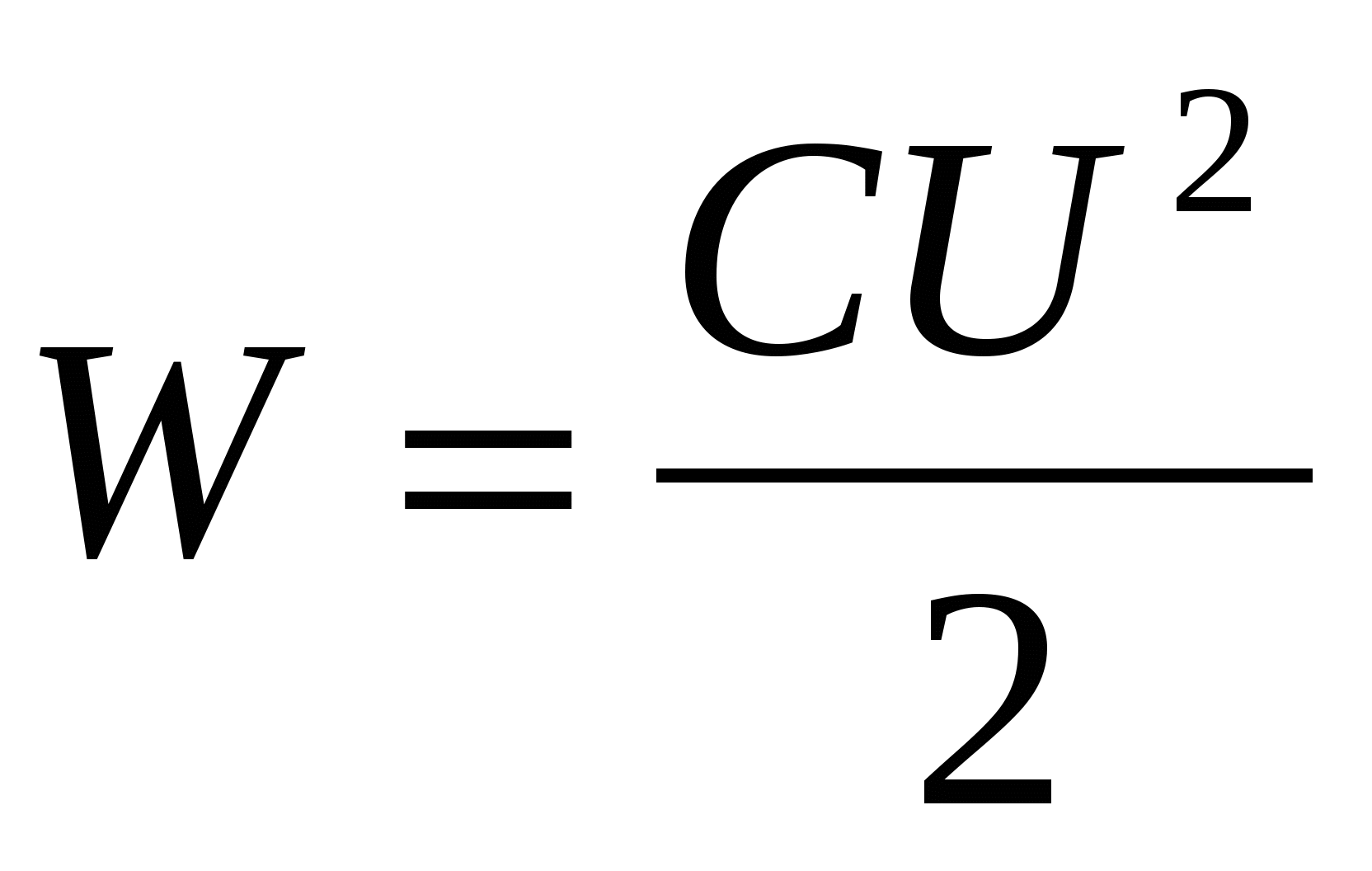 | (14.10) |
Дальнейшее рассмотрение проведём, основываясь на формуле (14.9). Представим заряд конденсатора как Q= S , где – поверхностная плотность заряда, а S – площадь обкладки конденсатора. Воспользовавшись далее выражением для ёмкости плоского конденсатора (13.7), представим (14.9) в виде
В формуле (14.9) энергия заряженного конденсатора выражена через заряд на его обкладках и ёмкость. В формуле (14.12) энергия конденсатора выражена через напряжённость электростатического поля, сосредоточенного между его обкладками. В связи с этим возникает принципиальный вопрос о том, что служит носителем энергии конденсатора: заряды или электростатическое поле. Этот вопрос – центральный в длительной дискуссии между сторонниками дальнодействия и близкодействия.
Сторонники дальнодействия отдавали предпочтение формуле (14.9), рассматривая её как потенциальную энергию взаимодействия двух тел. Приверженцы этой теории отвергали возможность осуществления взаимодействия посредством поля.
Сторонники теории близкодействия (полевой теории) считали, что энергия конденсатора есть энергия электростатического поля (формула (14.2)). Эта энергия "размазана" по всему объёму конденсатора и, следовательно, можно говорить об объёмной плотности энергии:
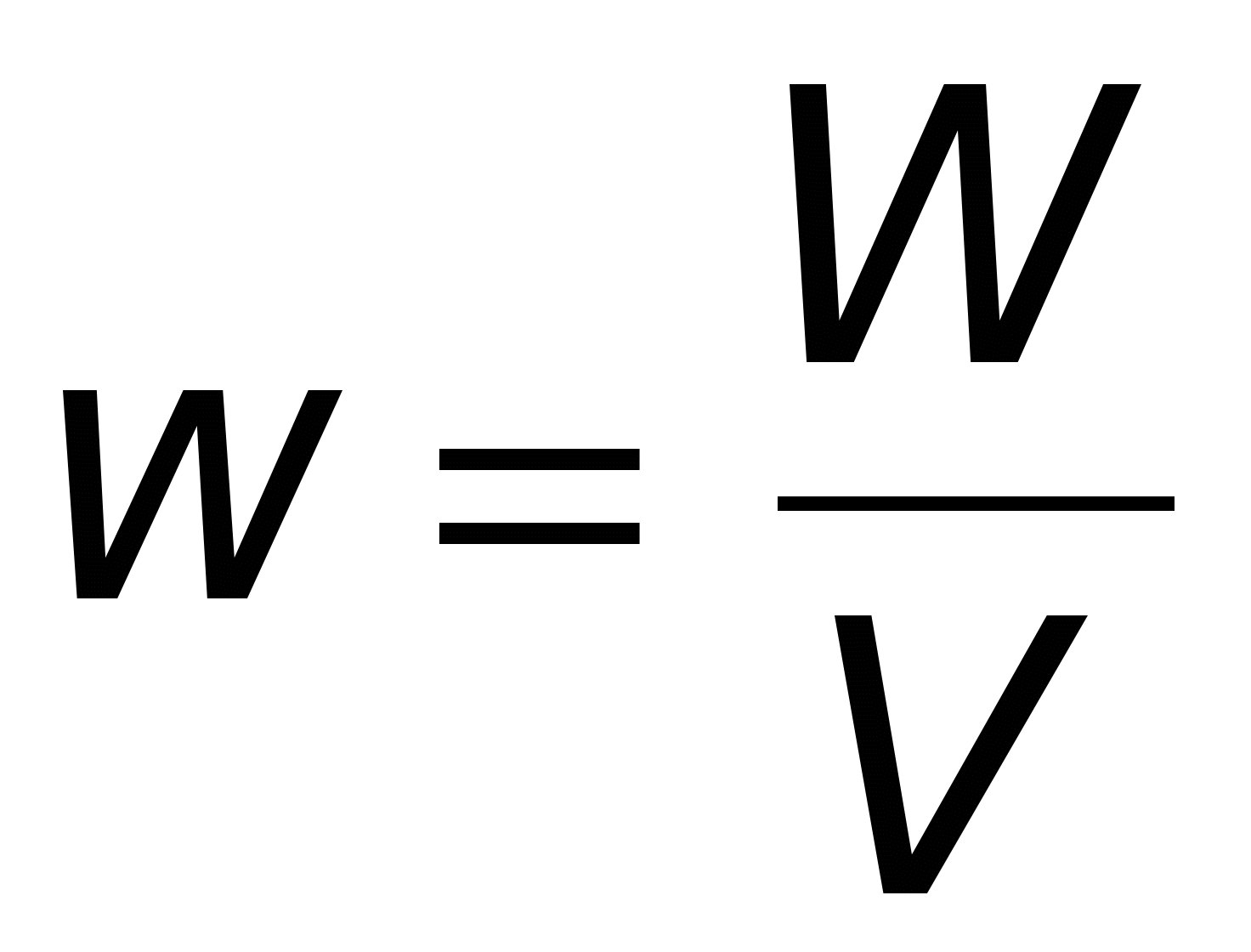 [Дж/м 3 ] или
[Дж/м 3 ] или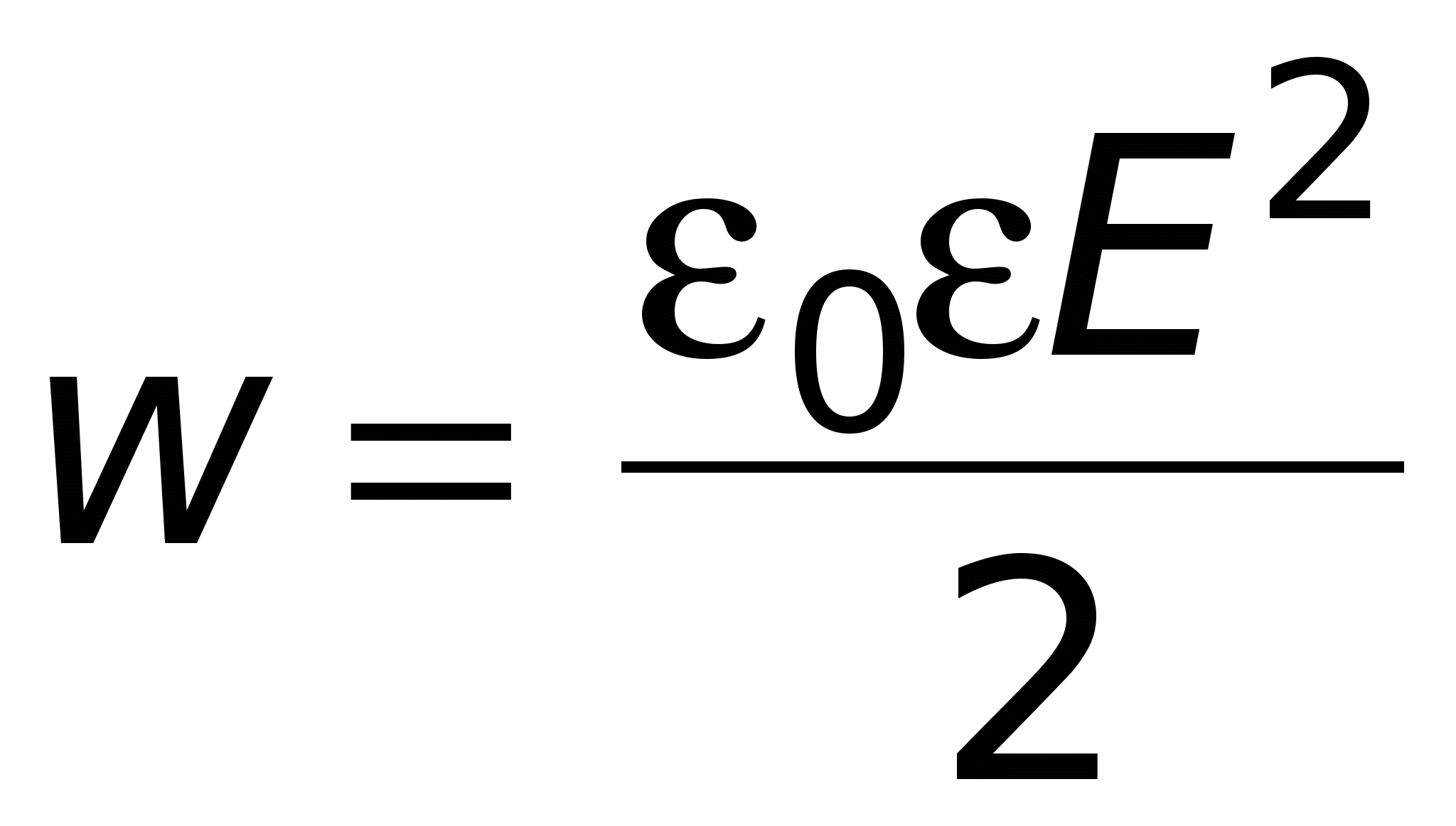 , С учётом (12.11) формулу (14.13) можно представить в виде
, С учётом (12.11) формулу (14.13) можно представить в виде
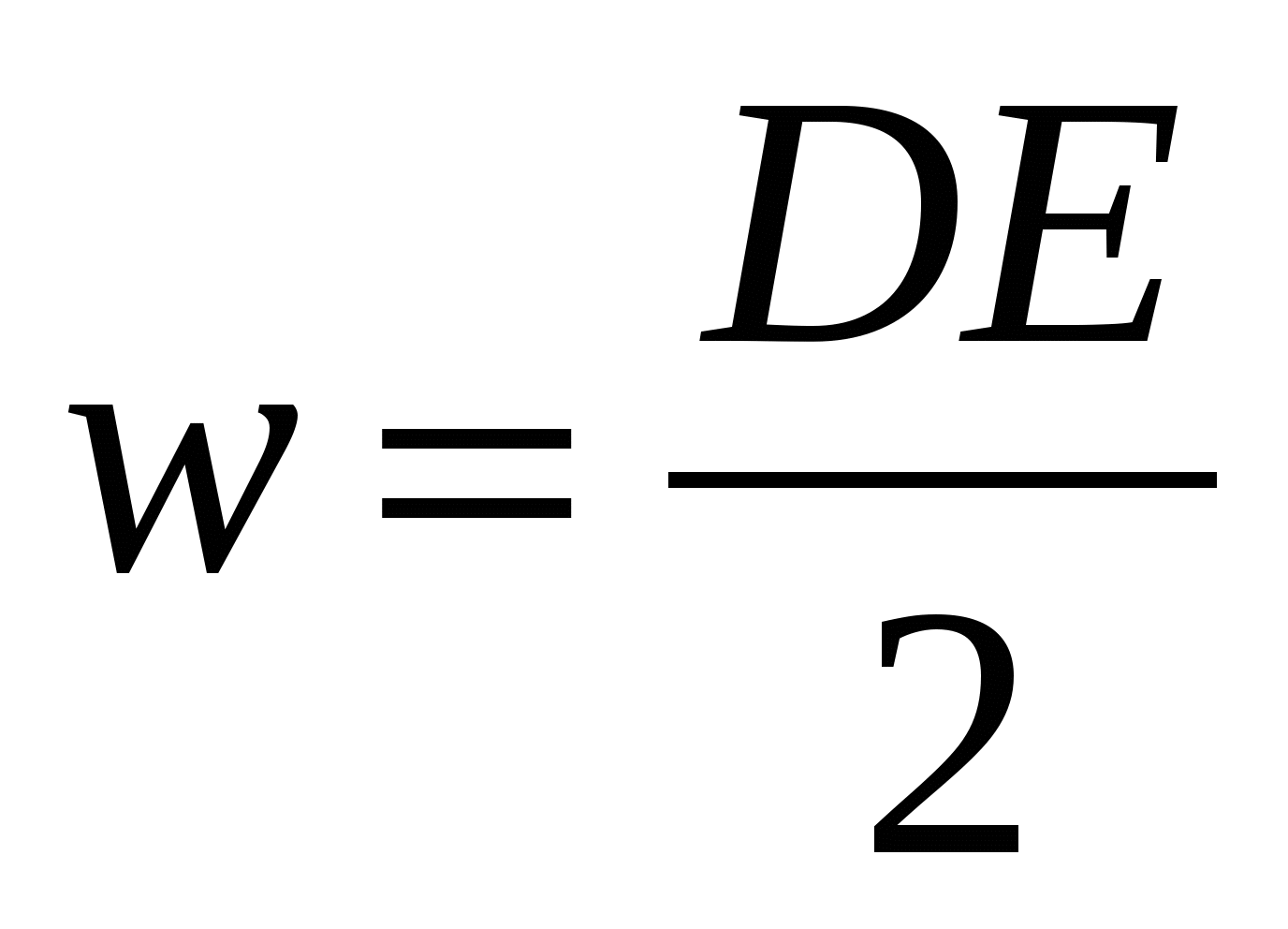 | (14.14) |
В рамках электростатики решить вопрос, что является носителем энергии – заряды или поле, невозможно, поскольку неподвижные заряды и создаваемое ими электростатическое поле неотделимы друг от друга. При изучении переменных электрических и магнитных полей оказалось, что электромагнитное поле может отрываться от зарядов, существуя независимо от них. Это и есть решающий аргумент в пользу теории близкодействия (полевой теории).
Лекція 23.
15. Постоянный электрический ток
^
15.1. Сила и плотность тока
Электрическим током называют упорядоченное (направленное) движение заряженных микрочастиц или заряженных макроскопических тел. За направление тока принимают направление движения положительных зарядов; если ток создается отрицательно заряженными частицами (например, электронами), то направление тока противоположно направлению движения частиц. Различают ток проводимости (направленное движение заряженных частиц внутри макроскопического тела) и конвекционный (движение заряженного тела как целого). В дальнейшем будем рассматривать лишь ток проводимости.
Количественно электрический ток характеризуется скалярной величиной силой тока I
и векторной величиной – плотностью электрического тока 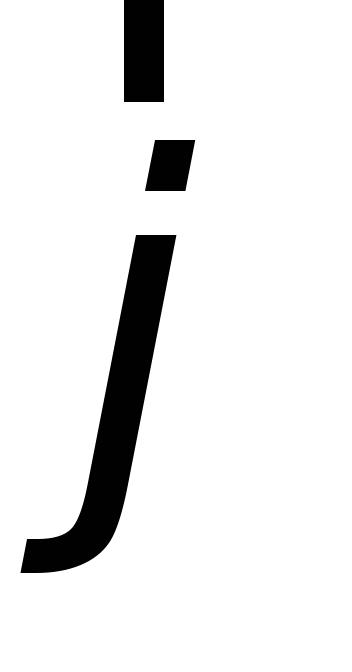 .
.
Сила тока численно равна заряду, прошедшему через поперечное сечение проводника за единицу времени:
где знак "" обозначает, что площадка 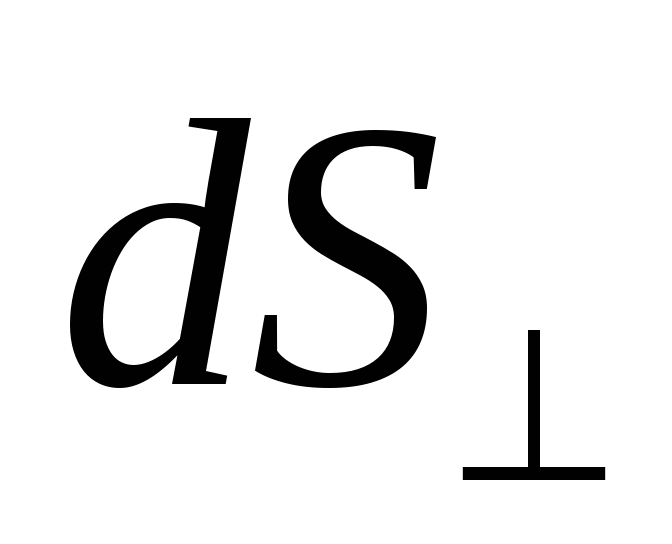 ориентирована перпендикулярно к направлению тока. Направление вектора
совпадает с направлением движения положительных зарядов.
ориентирована перпендикулярно к направлению тока. Направление вектора
совпадает с направлением движения положительных зарядов.
Найдем выражение для вектора плотности тока в металлах, у которых носителями тока являются свободные электроны. Под действием электрического поля электроны в металле движутся направлено со средней скоростью 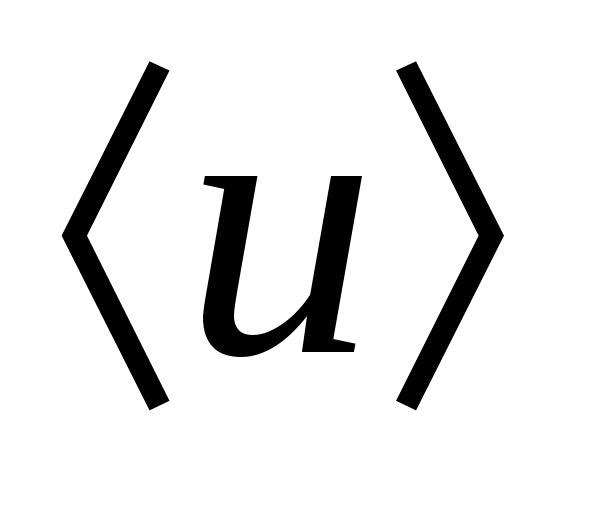 . За единицу времени через единичную площадку поперечного сечения проводника пройдет n
электронов, где n
– число электронов в единице объема (концентрация). При этом будет перенесен заряд en
. Следовательно плотность тока
. За единицу времени через единичную площадку поперечного сечения проводника пройдет n
электронов, где n
– число электронов в единице объема (концентрация). При этом будет перенесен заряд en
. Следовательно плотность тока
 . . | (15.3) |
15.2. Условия существования тока. Сторонние силы. ЭДС
Если вектор плотности тока не изменяется с течением времени ни по величине, ни по направлению, то такой ток называется постоянным. Найдем условия существования постоянного тока.
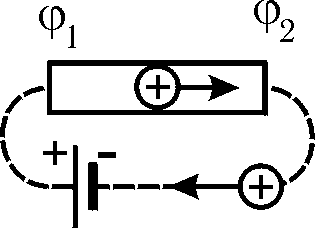
Рис. 15.1
Предположим, что на концах проводника создана разность потенциалов 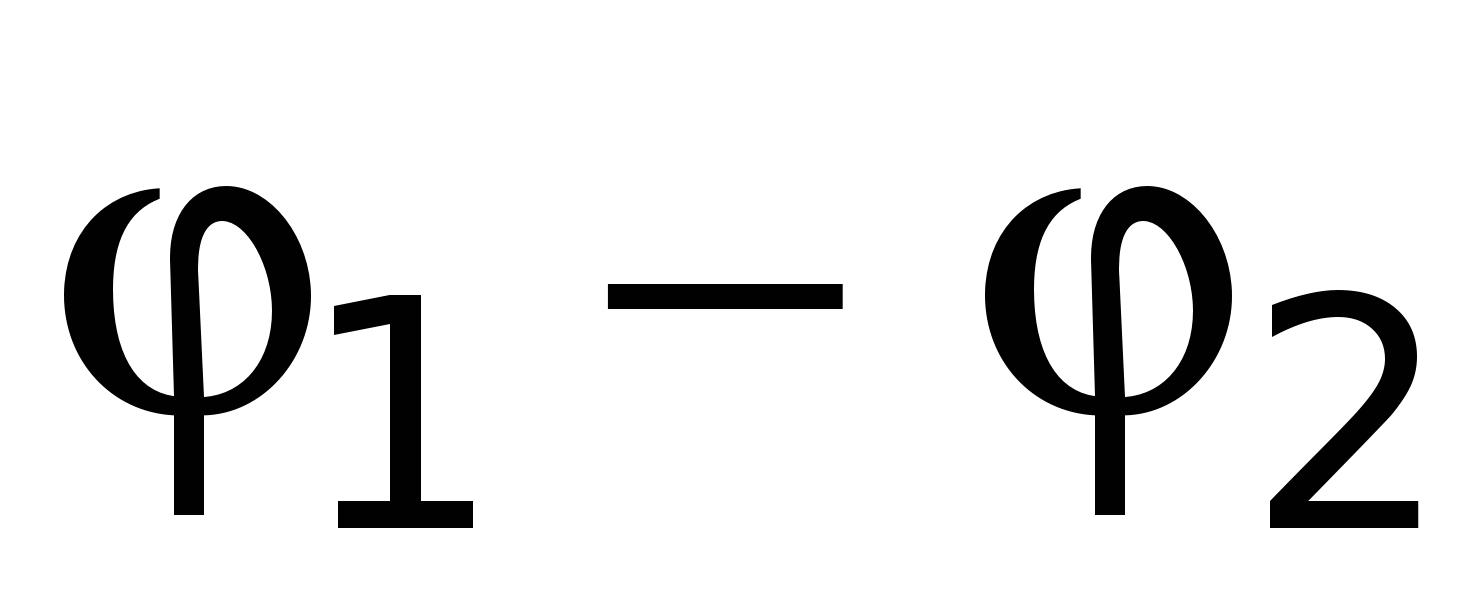 , причем
, причем 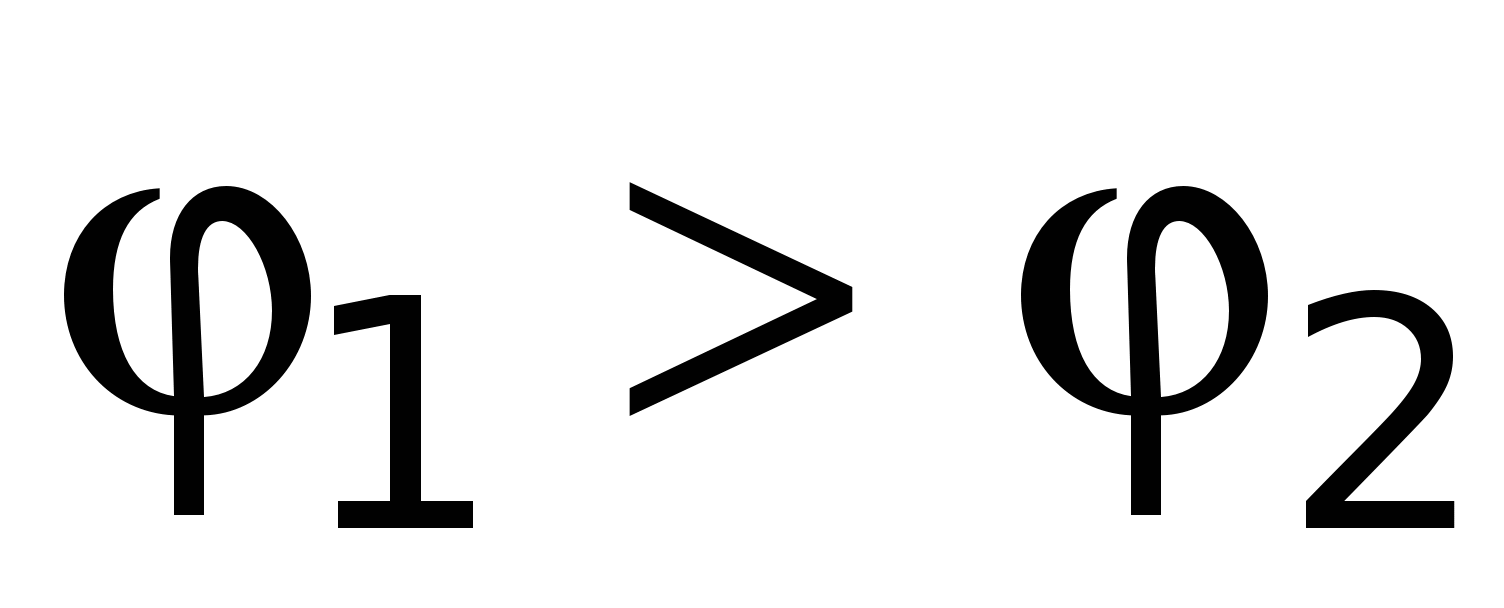 (рис. 15.1). При этом в проводнике возникнет кратковременный ток, вызванный упорядоченным движением зарядов в сторону убыли потенциала (предполагается, что носители тока имеют положительный заряд). Ток будет существовать до тех пор, пока не произойдет выравнивание потенциалов на концах проводника, Для того же, чтобы ток сохранялся постоянным в течение длительного времени, необходимо от конца проводника с меньшим потенциалом отводить заряды к концу проводника с большим потенциалом, т.е. осуществлять кругооборот зарядов. В связи с этим цепь должна быть замкнутой.
(рис. 15.1). При этом в проводнике возникнет кратковременный ток, вызванный упорядоченным движением зарядов в сторону убыли потенциала (предполагается, что носители тока имеют положительный заряд). Ток будет существовать до тех пор, пока не произойдет выравнивание потенциалов на концах проводника, Для того же, чтобы ток сохранялся постоянным в течение длительного времени, необходимо от конца проводника с меньшим потенциалом отводить заряды к концу проводника с большим потенциалом, т.е. осуществлять кругооборот зарядов. В связи с этим цепь должна быть замкнутой.
Электростатические силы такой кругооборот зарядов обеспечить не могут, так как на участке цепи, показанном на рис. 15.1 пунктиром, нужно выполнять работу против электростатического поля. Перемещение зарядов в сторону возрастания потенциала возможно лишь с помощью дополнительных сил неэлектростатического происхождения, называемых сторонними силами. Эти силы могут быть обеспечены химическими процессами (гальванические элементы), вихревым электрическим полем (генераторы переменного или постоянного тока) и т.д.
В отличие от электростатических сил, работа сторонних сил по перемещению заряда по замкнутому кругу отлична от нуля. Электродвижущей силой (ЭДС) называется работа, совершаемая сторонними силами по перемещению единичного положительного заряда по всей цепи, 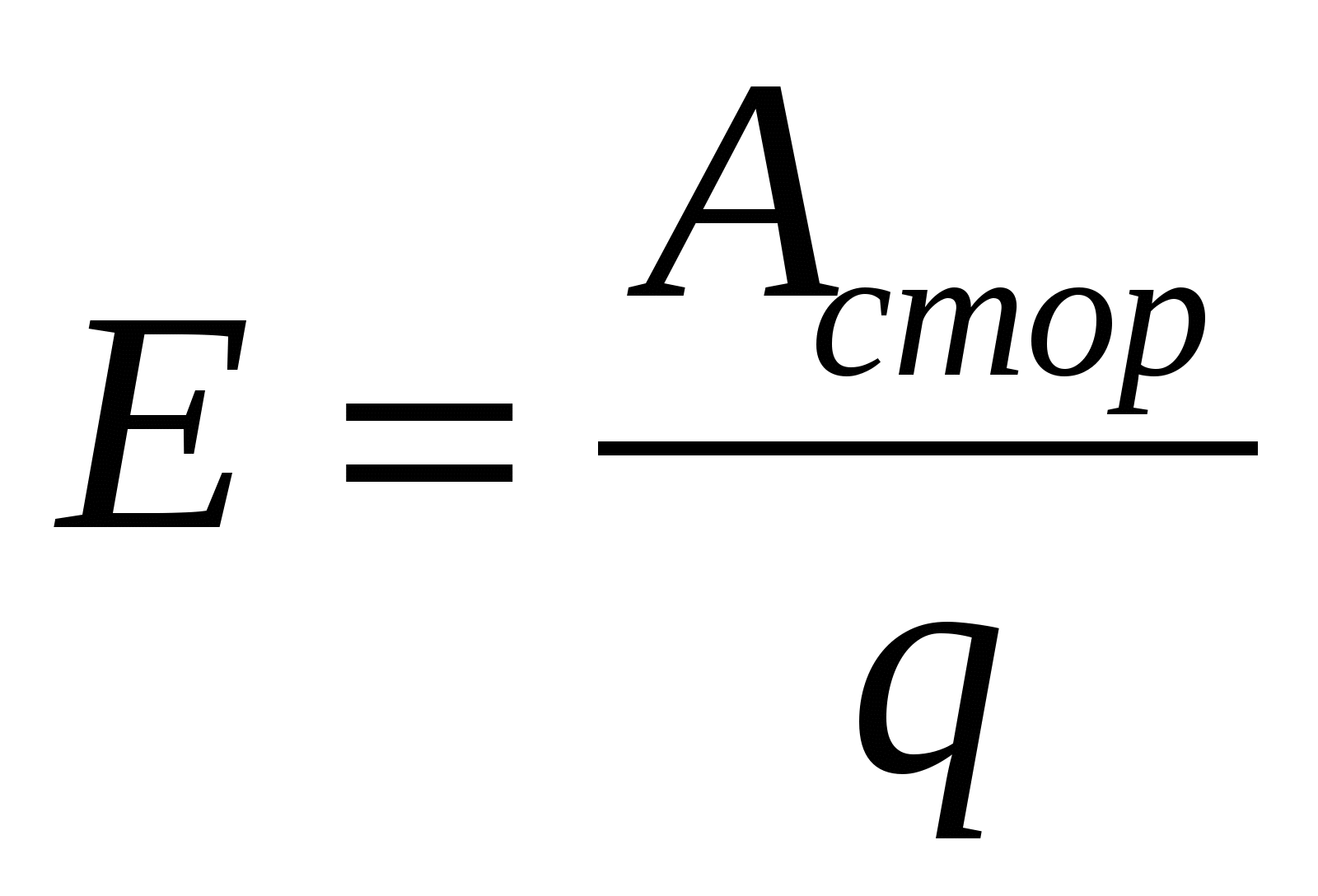 , (15.4) .Как и разность потенциалов, ЭДС измеряется в вольтах.
, (15.4) .Как и разность потенциалов, ЭДС измеряется в вольтах.
Рассмотрим участок цепи, на котором кроме сторонних сил действуют электростатические. Тогда работа по перемещению заряда на этом участке будет равна сумме работ: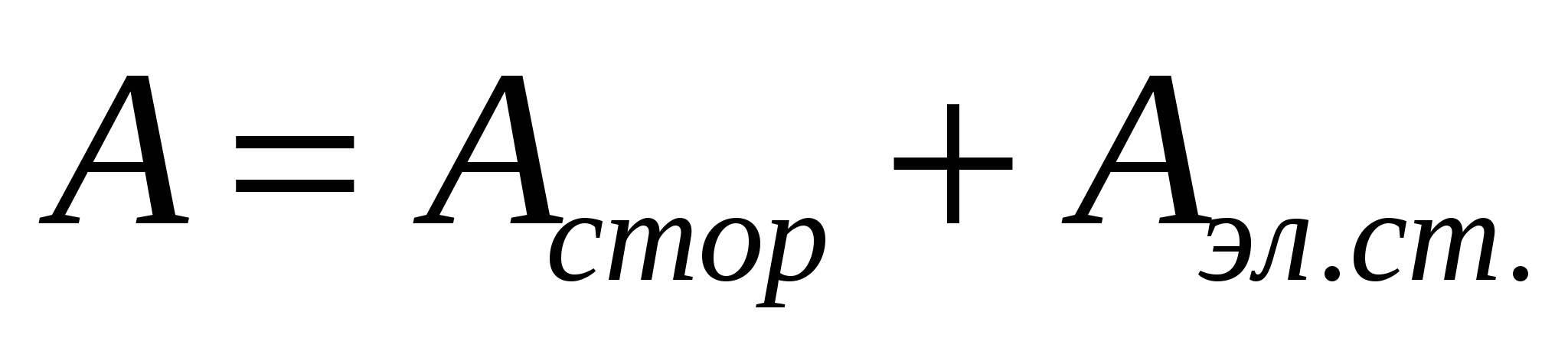
Разделим это выражение на заряд q
:
Суммарная работа, выполняемая как сторонними, так и электростатическими силами по перемещению единичного положительного заряда на некотором участке цепи, называется напряжением или падением напряжения:
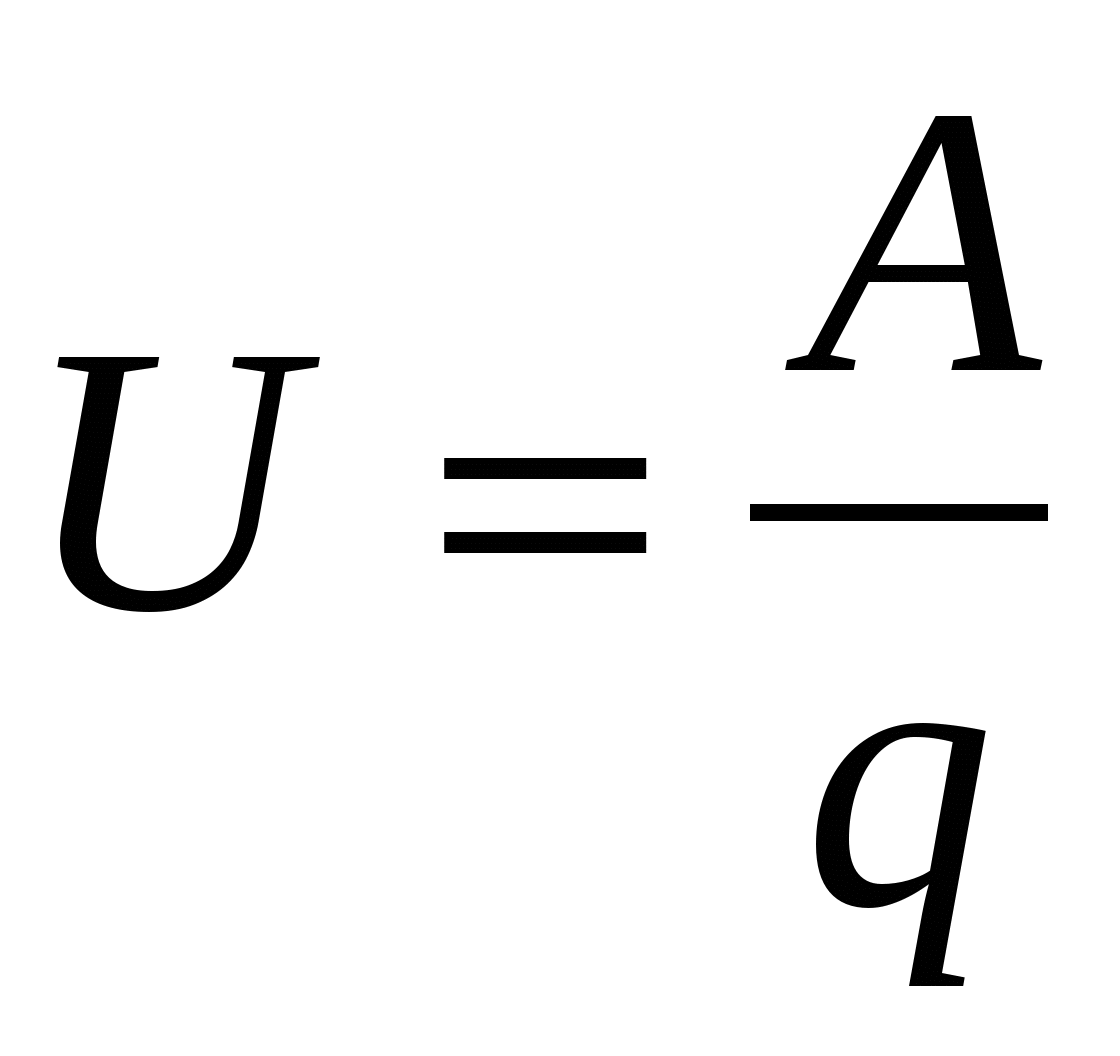 . . | (15.7) |
Подставив (15.4), (15.6) и (15.7) в (15.5), получим связь между напряжением, ЭДС и разностью потенциалов U=E + ( 1 - 2 )
Из (15.8) видно, что напряжение U
равно алгебраической сумме ЭДС и разности потенциалов на данном участке цепи.
^
15.3. Закон Ома
15.3.1. Закон Ома для неоднородного участка цепи
Ом экспериментально установил, что сила тока на некотором участке цепи пропорциональна напряжению и обратно пропорциональна сопротивлению: 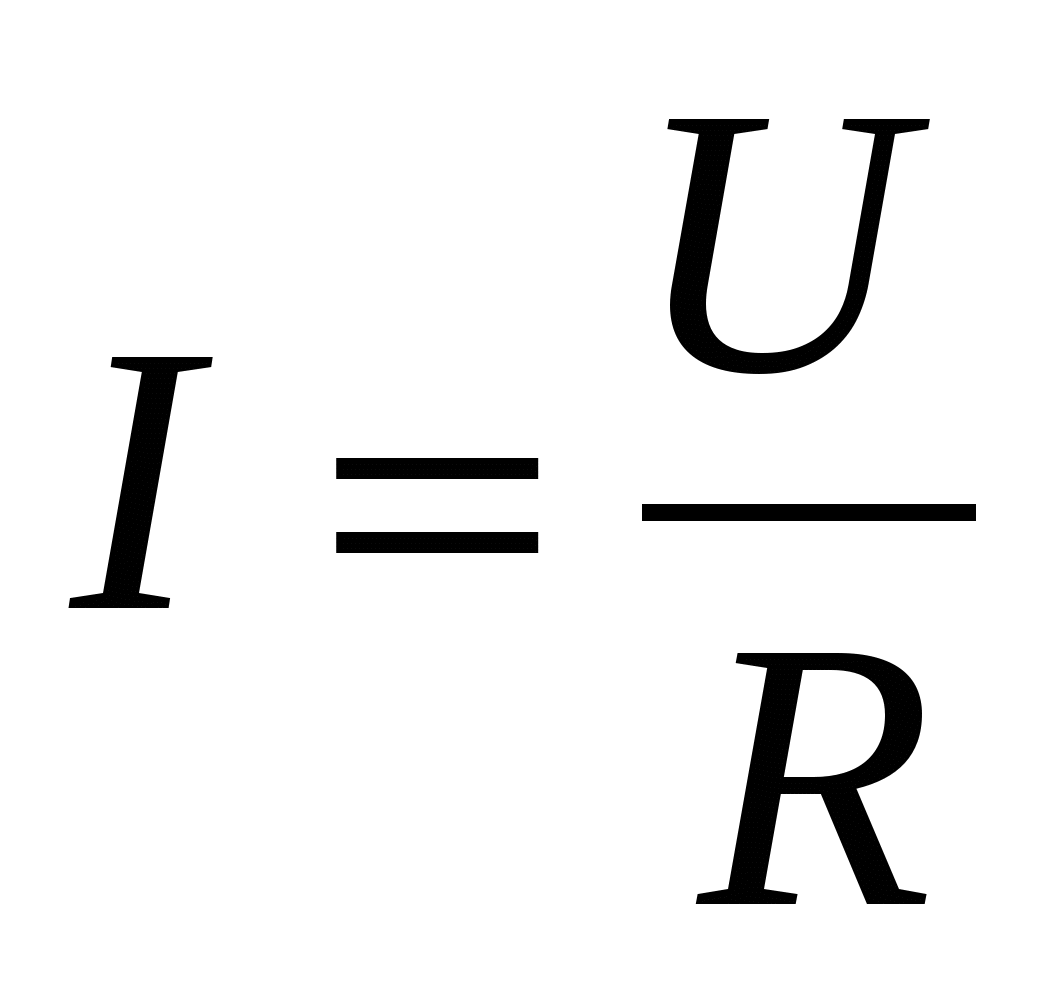 . . | (15.9) |
Найдем из (15.9) напряжение U и подставим в (15.8): IR = E +( 1 – 2 ) , (15.10)
Полученное выражение есть закон Ома для неоднородного участка цепи, т.е. участка цепи, содержащего ЭДС.
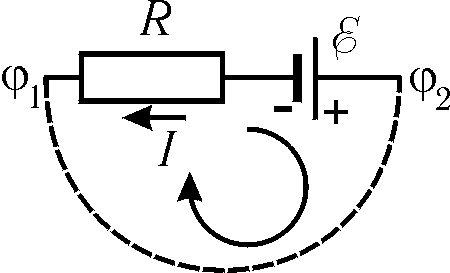
Рис. 15.2
При практическом использовании формулы (15.10) нужно установить знаки для напряжения и ЭДС. Для этого произвольным образом устанавливаем направление обхода (на рис. 15.2 направление обхода выбрано по часовой стрелке). Если направление тока совпадает с направлением обхода, то он берется со знаком "+", в противном случае его нужно взять со знаком "-". На рис. 15.2 направление обхода и направление тока не совпадают, поэтому в формуле (15.10) IR
берем со знаком "минус".
Остальная часть замкнутого контура на рис. 15.2 показана пунктиром. ЭДС по внешней цепи "перегоняет" заряды от своего "плюса" к "минусу". Ее нужно брать со знаком "+", если она действует в направлении обхода и со знаком "–" в противном случае. В соответствии с этим на схеме, изображенной на рис. 15.2, ЭДС нужно взять со знаком "+". Таким образом, закон Ома для неоднородного участка цепи в данном случае запишем в виде: –
IR
=
E
+(
1
–
2
)
.
^
15.3.2. Закон Ома для полной цепи
При обходе полной цепи начальная и конечная точки совпадают, поэтому  ;
;
^
15.3.3. Закон Ома для однородного участка цепи
Однородным называется участок цепи, не содержащий источника ЭДС, т.е. в формуле (15.10) нужно положить E
=0
. Тогда 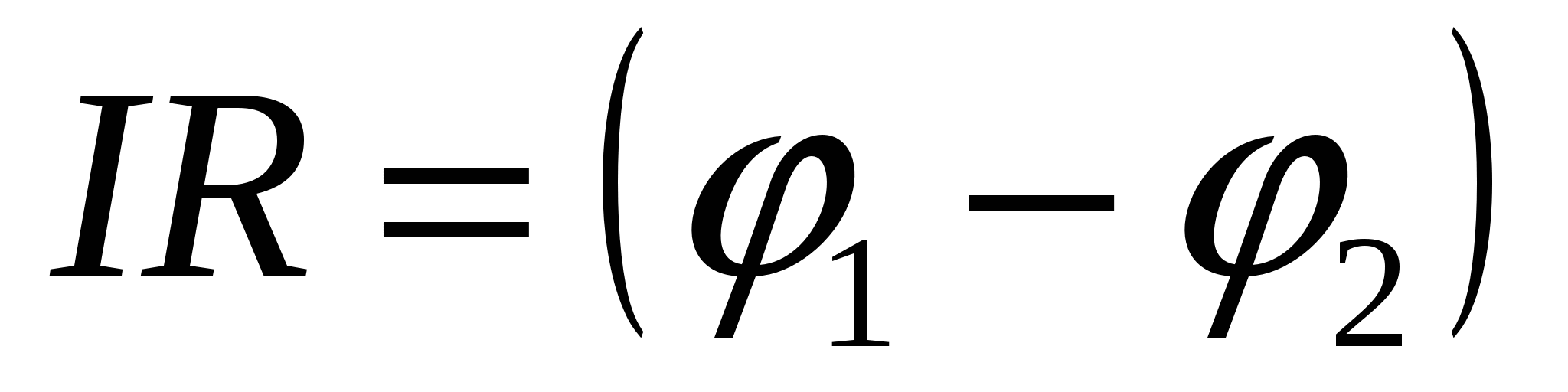 .
.
В данном случае падение напряжения совпадает с разностью потенциалов U
= 1 - 1 , т. е.
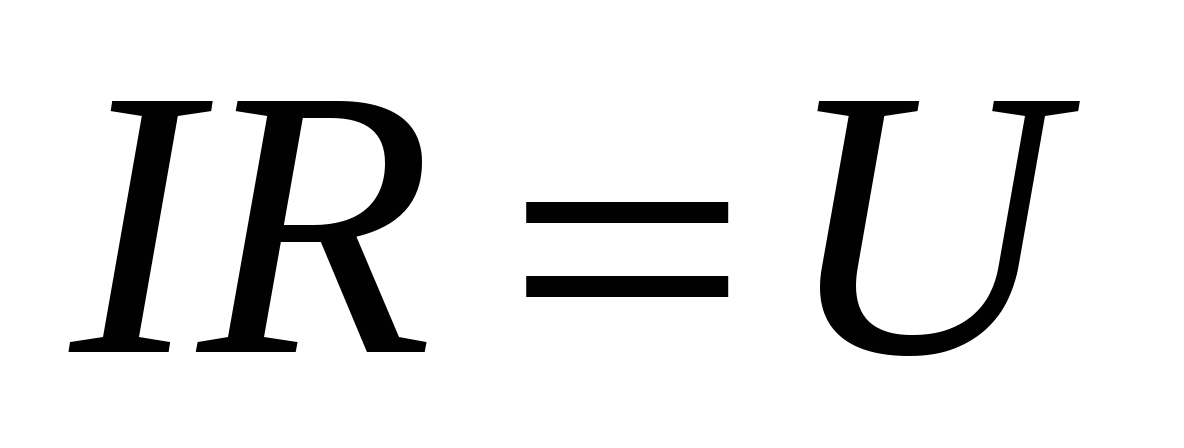 , , | (15.13) |
что также совпадает с (15.9).
Формулы (15.9) и (15.13) представляют закон Ома в интегральной форме.
^
15.3.4. Закон Ома в дифференциальной форме
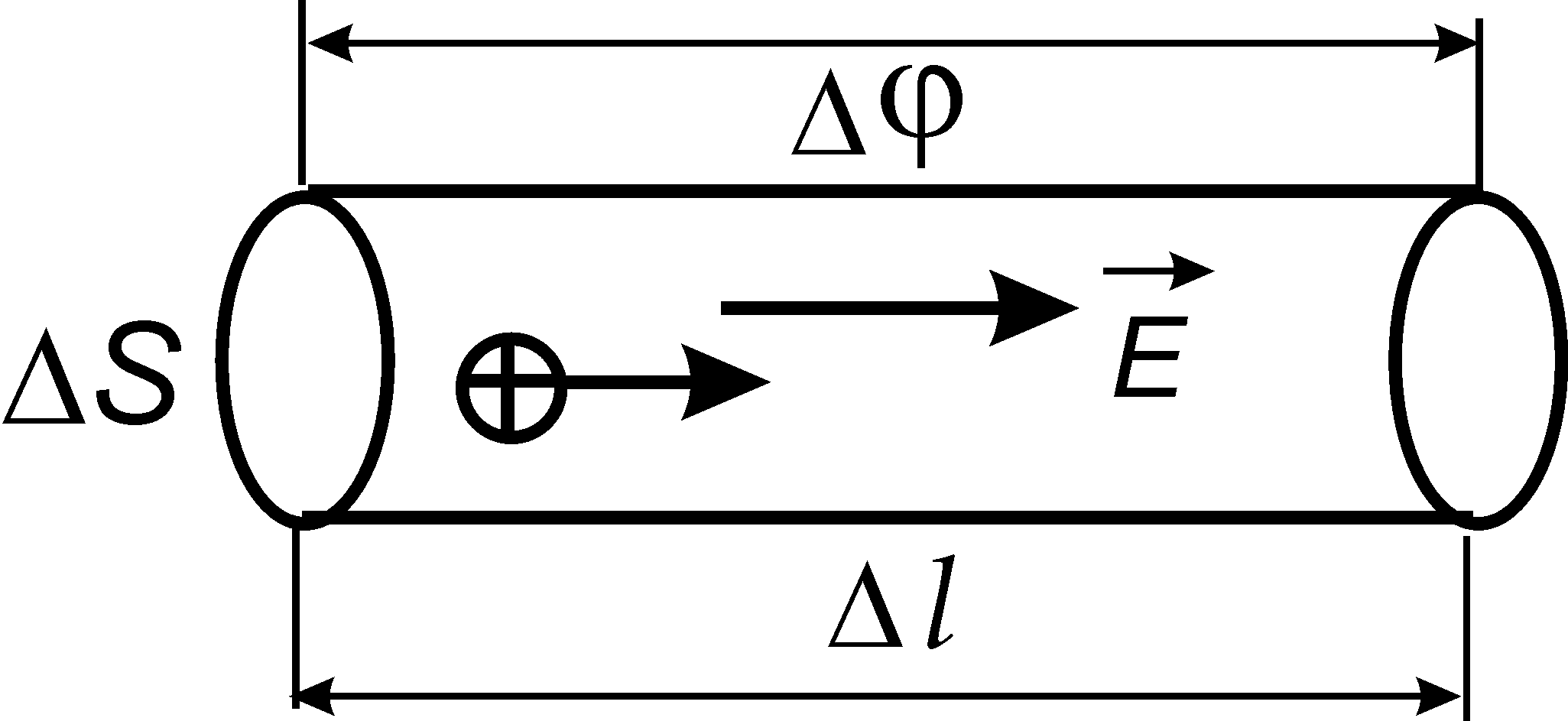
Рис. 5.3
Выделим внутри проводника с током элементарный цилиндр сечением S
и длиной l
(рис. 15.3). Сила тока в нем I
=S
, а его сопротивление 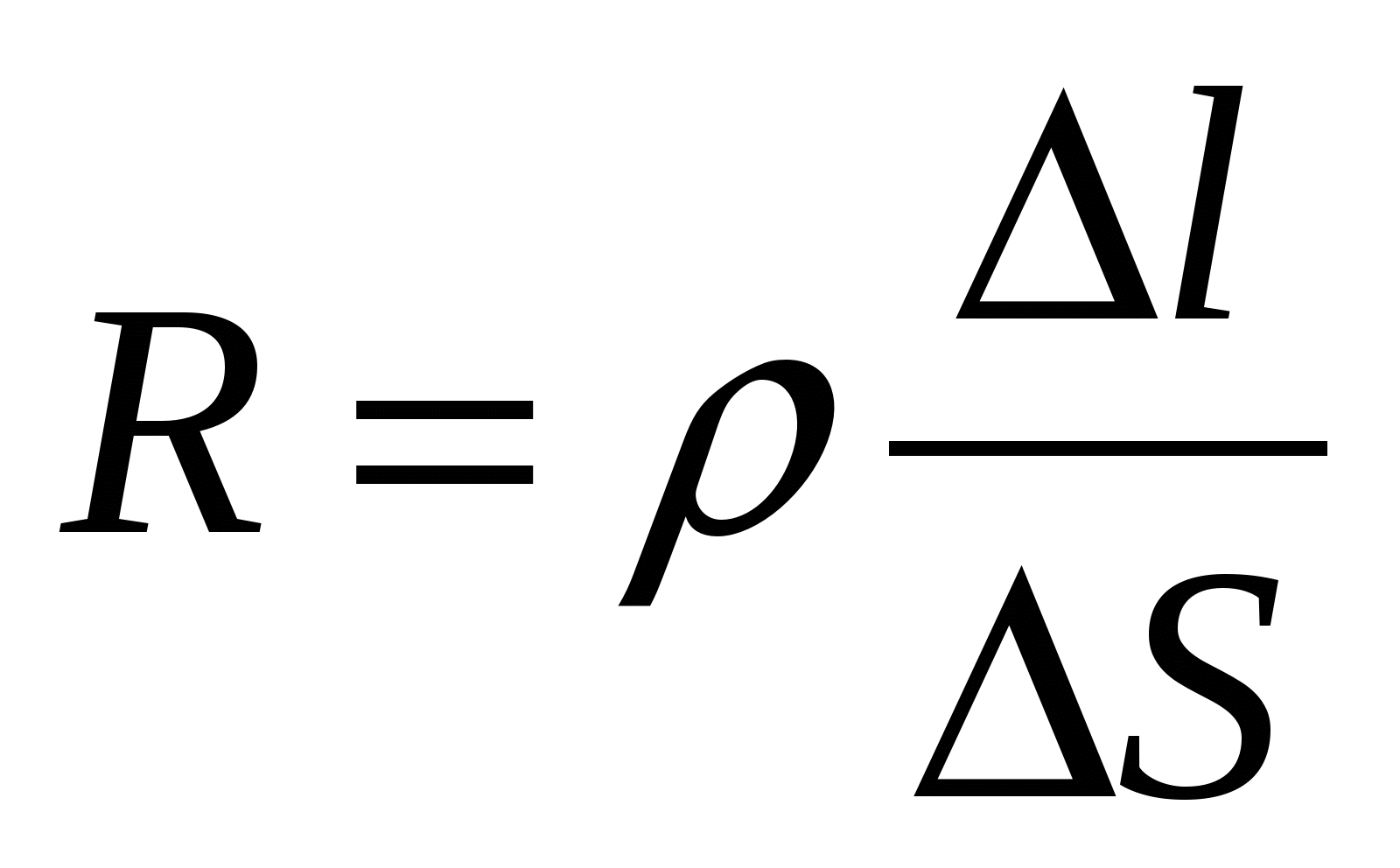 , где – удельное сопротивление проводника. Разность потенциалов на концах цилиндра . Тогда закон Ома (см. (15.9)) запишем в виде
, где – удельное сопротивление проводника. Разность потенциалов на концах цилиндра . Тогда закон Ома (см. (15.9)) запишем в виде
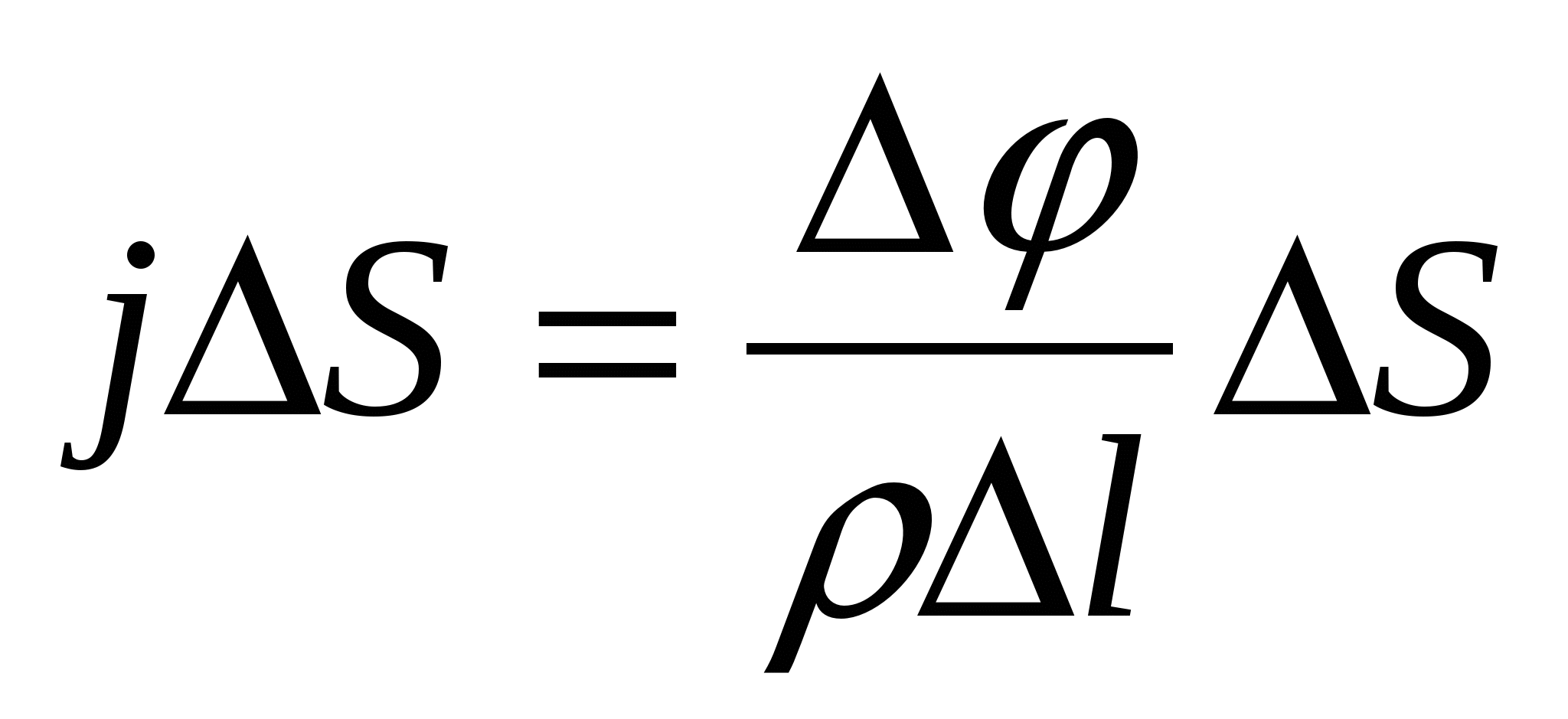 или .
или .
С учетом (11.30) последнее выражение можно преобразовать к виду
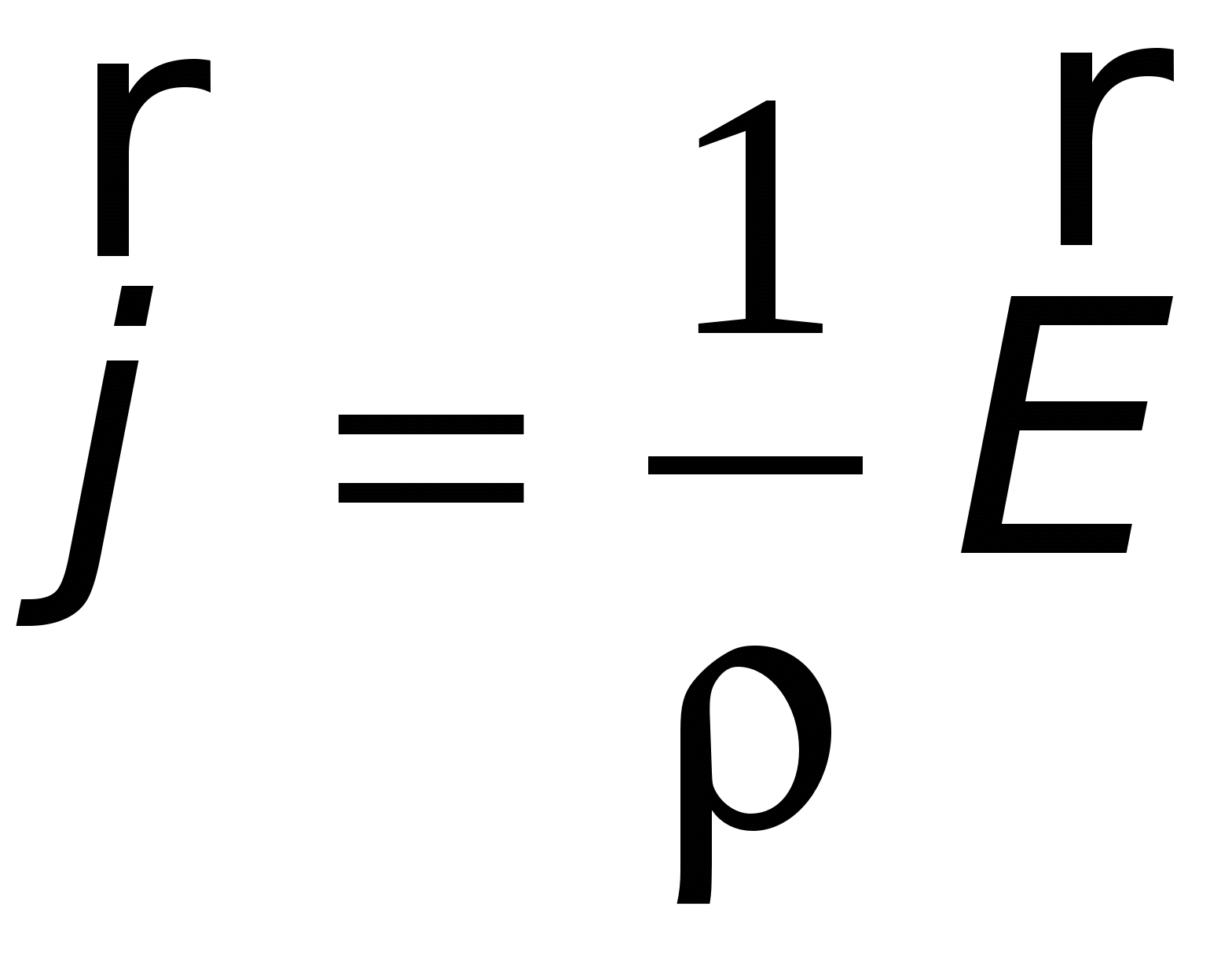 . . | (15.14) |
Величина, обратная удельному сопротивлению, называется удельной проводимостью:
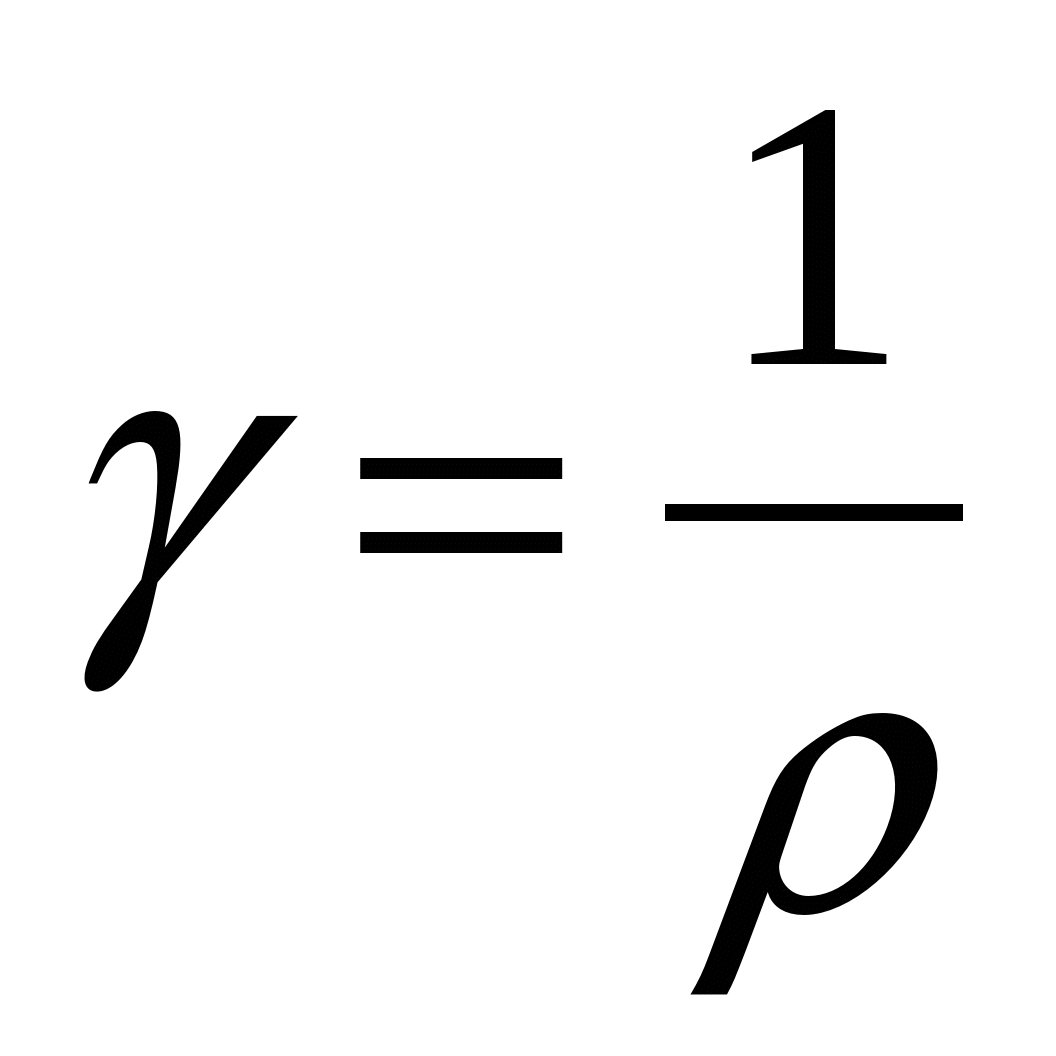 .
.Тогда закону Ома в дифференциальной форме (15.4) можно придать вид 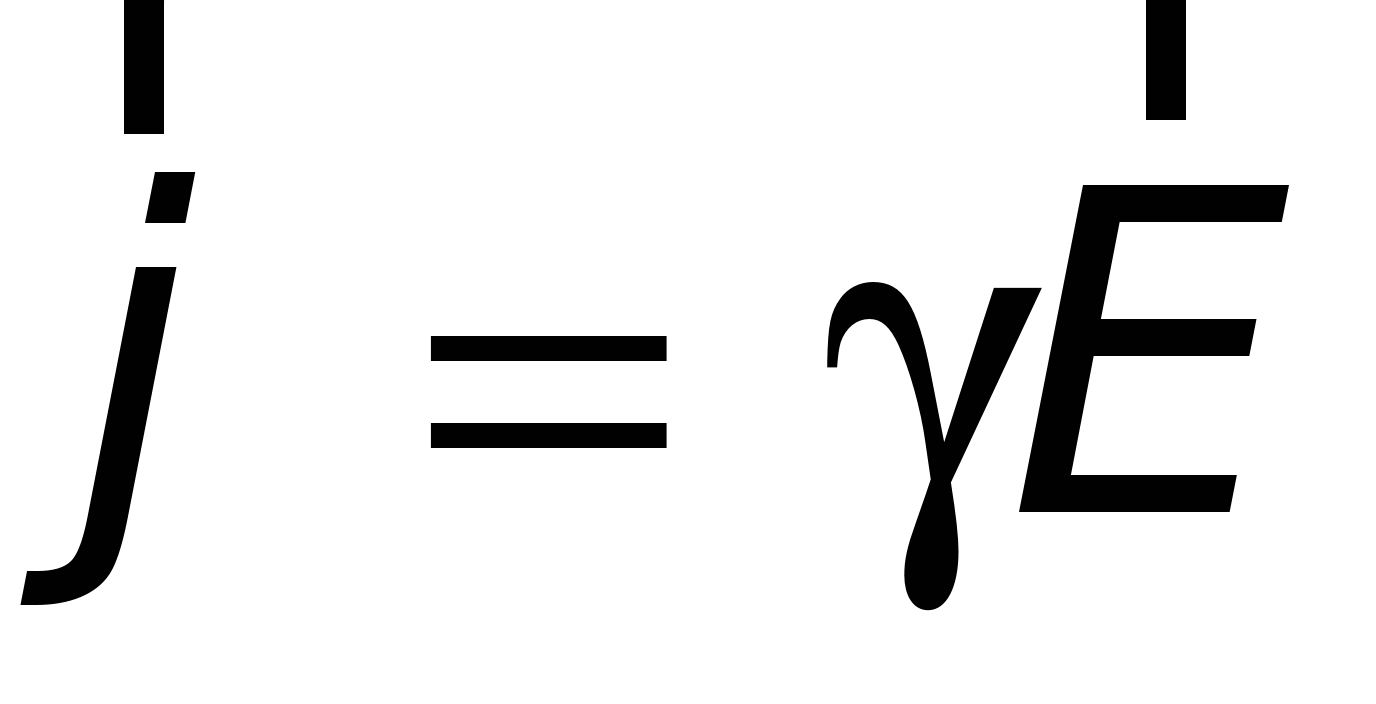
^
15.4. Закон Джоуля-Ленца
15.4.1. Закон Джоуля-Ленца в интегральной форме
Джоуль и независимо от него Ленц экспериментально установили, сто количество теплоты, выделенной в проводнике сопротивлением R за время dt , пропорционально квадрату силы тока, сопротивлению и времени: 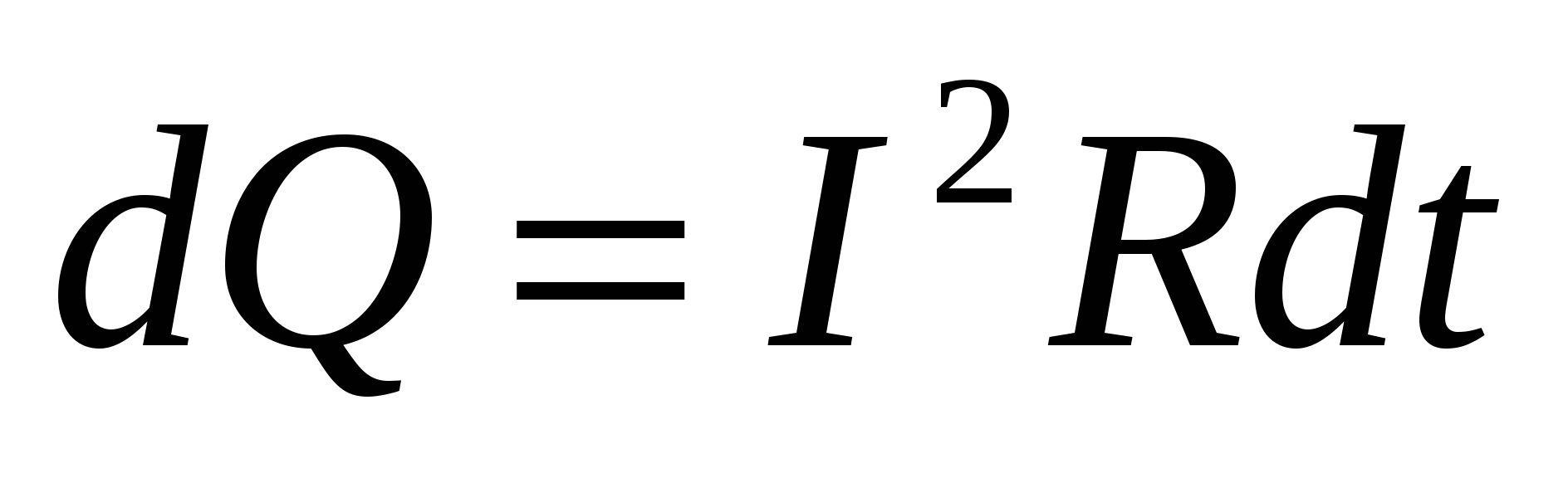 . . | (15.16) |
Формула (15.16) представляет закон Джоуля-Ленца в интегральной форме.
^
15.4.2. Закон Джоуля-Ленца в дифференциальной форме
Выделим, как и ранее, внутри проводника элементарный цилиндрический объем (рис. 15.3). Заменим в (15.16)
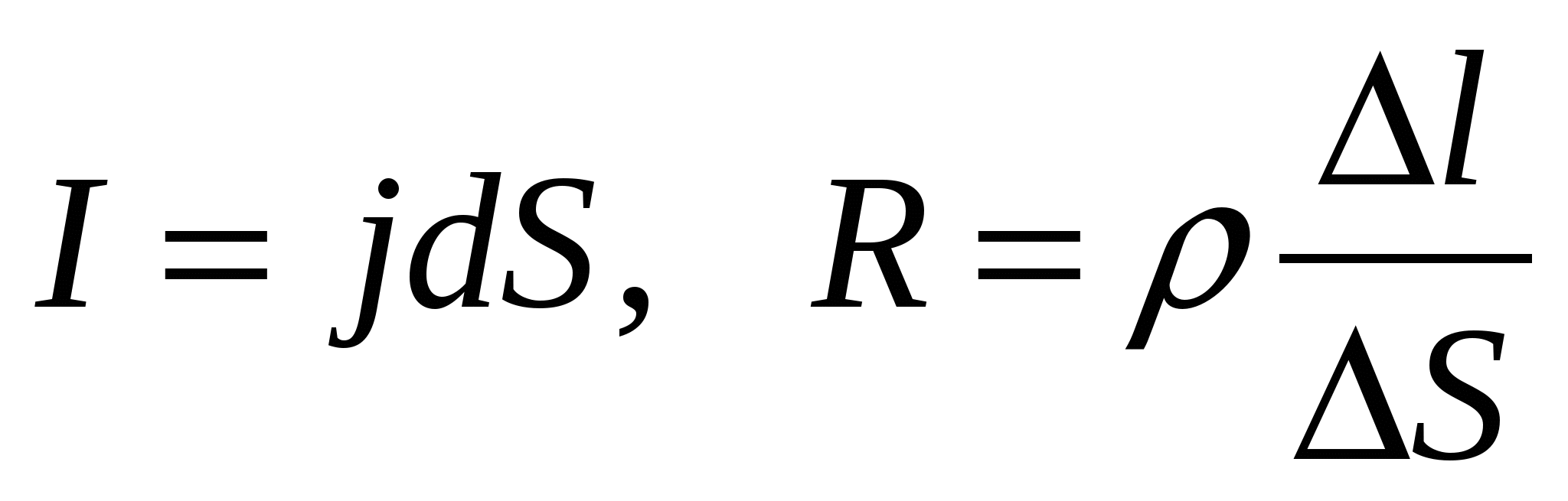 . Тогда
. Тогда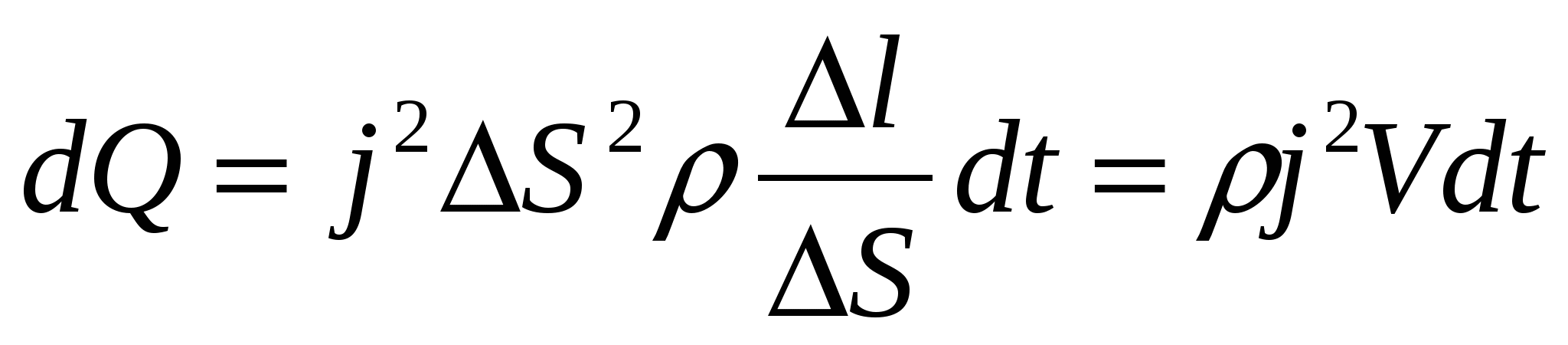 где V=
l
S
– объем проводника. Введем в рассмотрение удельную мощность теплоты
где V=
l
S
– объем проводника. Введем в рассмотрение удельную мощность теплоты 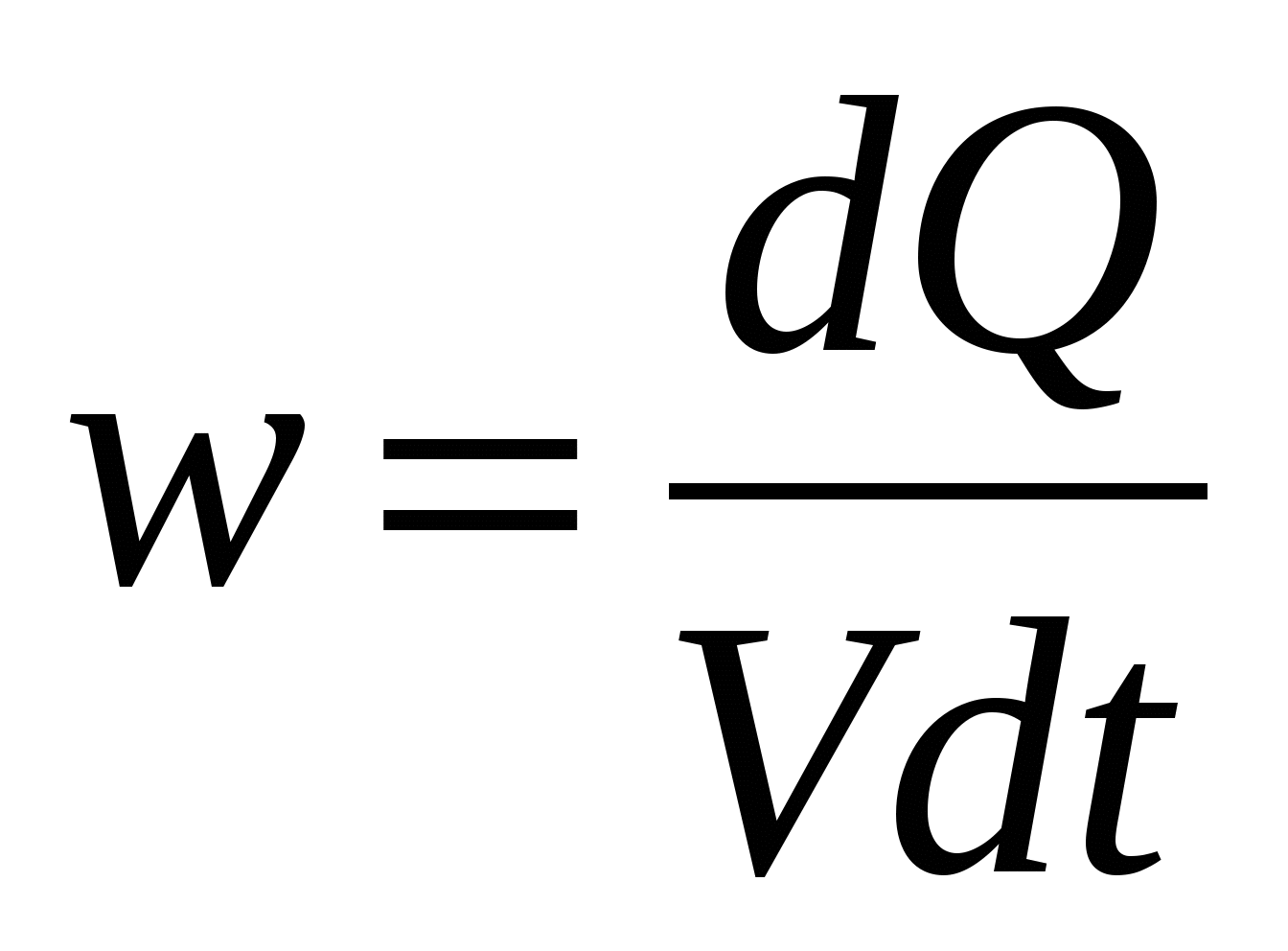 [Дж/м 3 с = Вт/м 3 ]. [Дж/м 3 с = Вт/м 3 ]. | (15.18) |
Удельная мощность теплоты численно равна количеству теплоты, выделенной в единице объема проводника за единицу времени. Другими словами – это тепловая мощность, развиваемая в единице объема. С учетом (15.18) выражению (15.17) можно придать вид
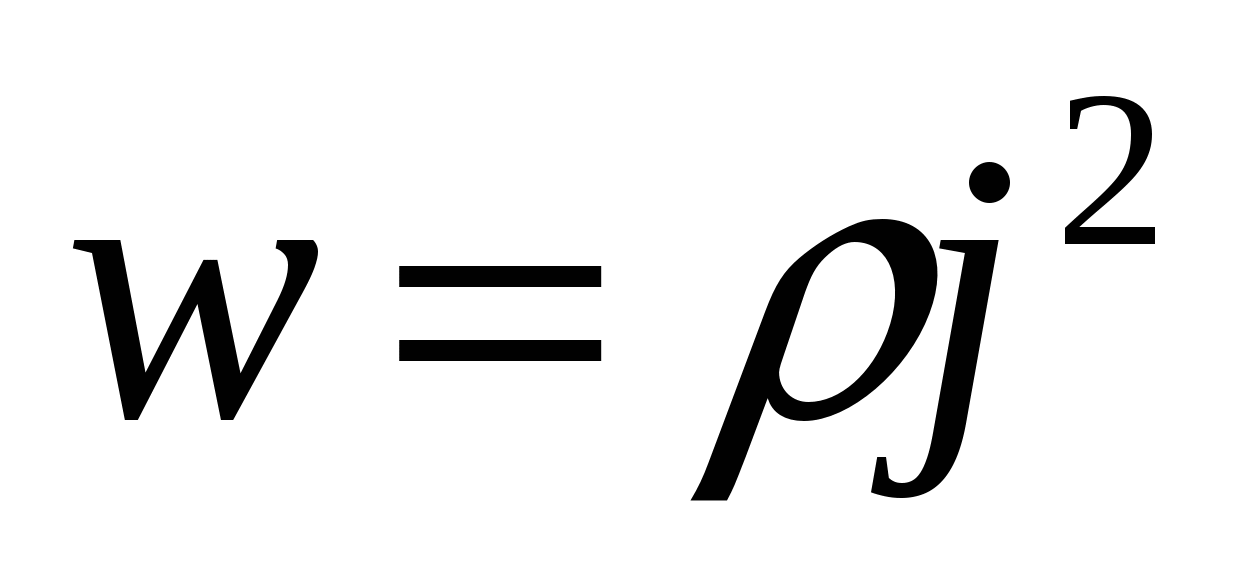 .
.
Формулы (15.19) и (15.20) представляют закон Джоуля-Ленца в дифференциальной форме.
Лекція 24.
^
15.5. Обоснование законов Ома и Джоуля-Ленца по классической электронной теории
В классической электронной теории металлов принимается следующая модель.
1. Носителями тока в металлах являются свободные электроны.
2. Свободные электроны образуют электронный газ, который по своим свойствам аналогичен идеальному газу. Имеется лишь одно различие: электроны при своем движении сталкиваются не между собой, а с ионами кристаллической решетки.
3. Под действием электрического поля электроны наряду с хаотическим движением со скоростью  начинают двигаться направлено со скоростью
начинают двигаться направлено со скоростью  . При этом скорость направленного движения значительно меньше скорости хаотического движения
. При этом скорость направленного движения значительно меньше скорости хаотического движения
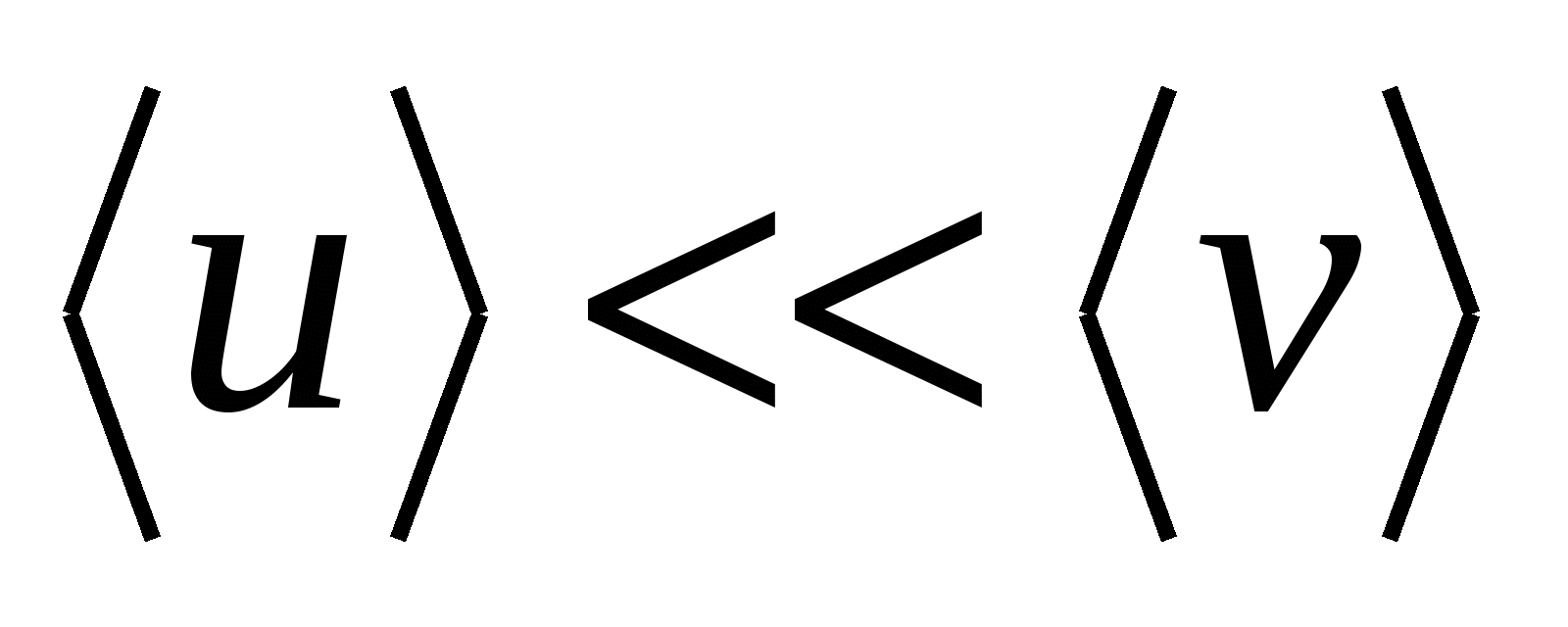 . . | (15.21) |
Найдем скорость направленного движения электронов. Предположим, что в момент времени t= 0 скорость направленного движения электронов u 0 =0. Под действием силы F=eE электрон в соответствии со вторым законом Ньютона начинает двигаться ускоренно:
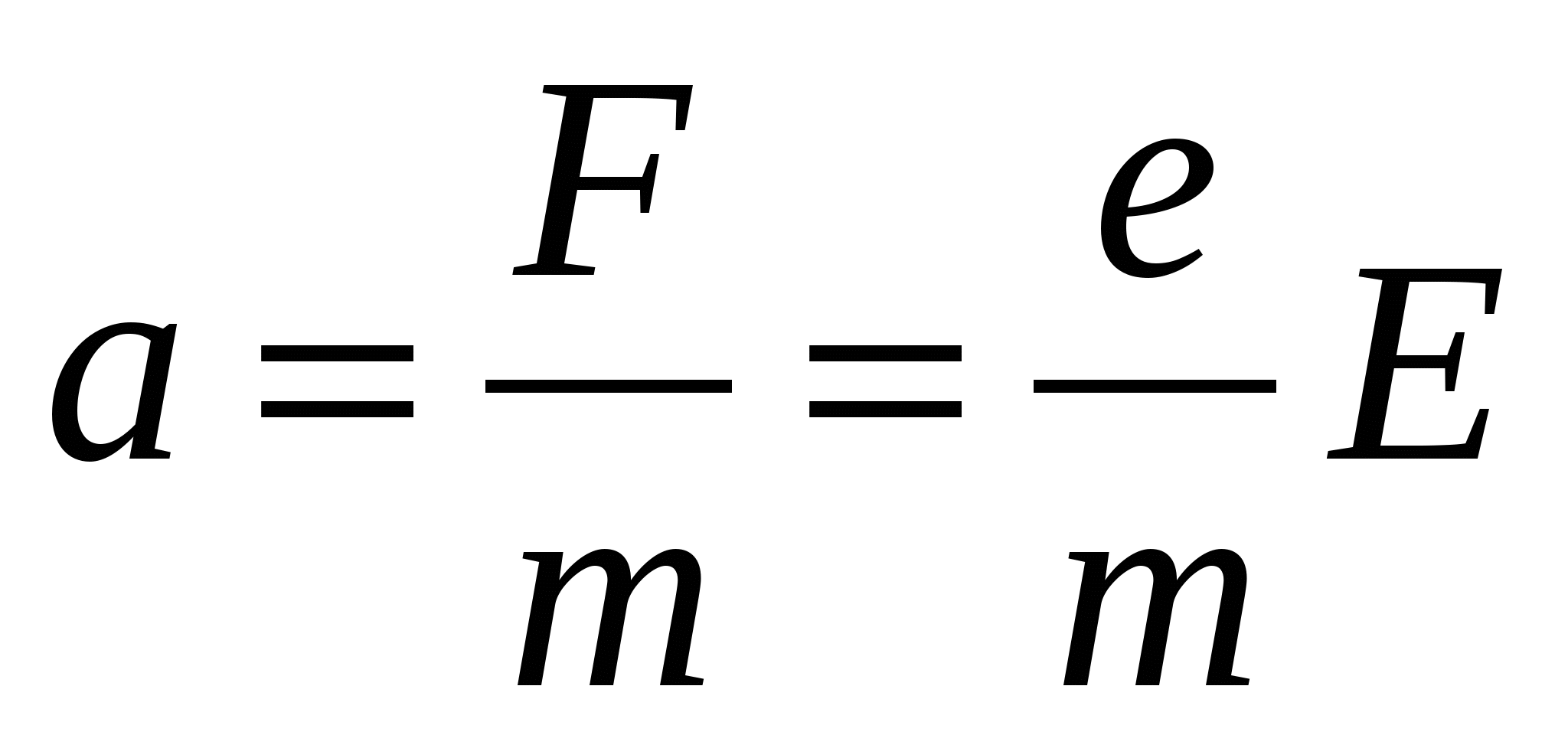 .
.
Скорость направленного движения электрона
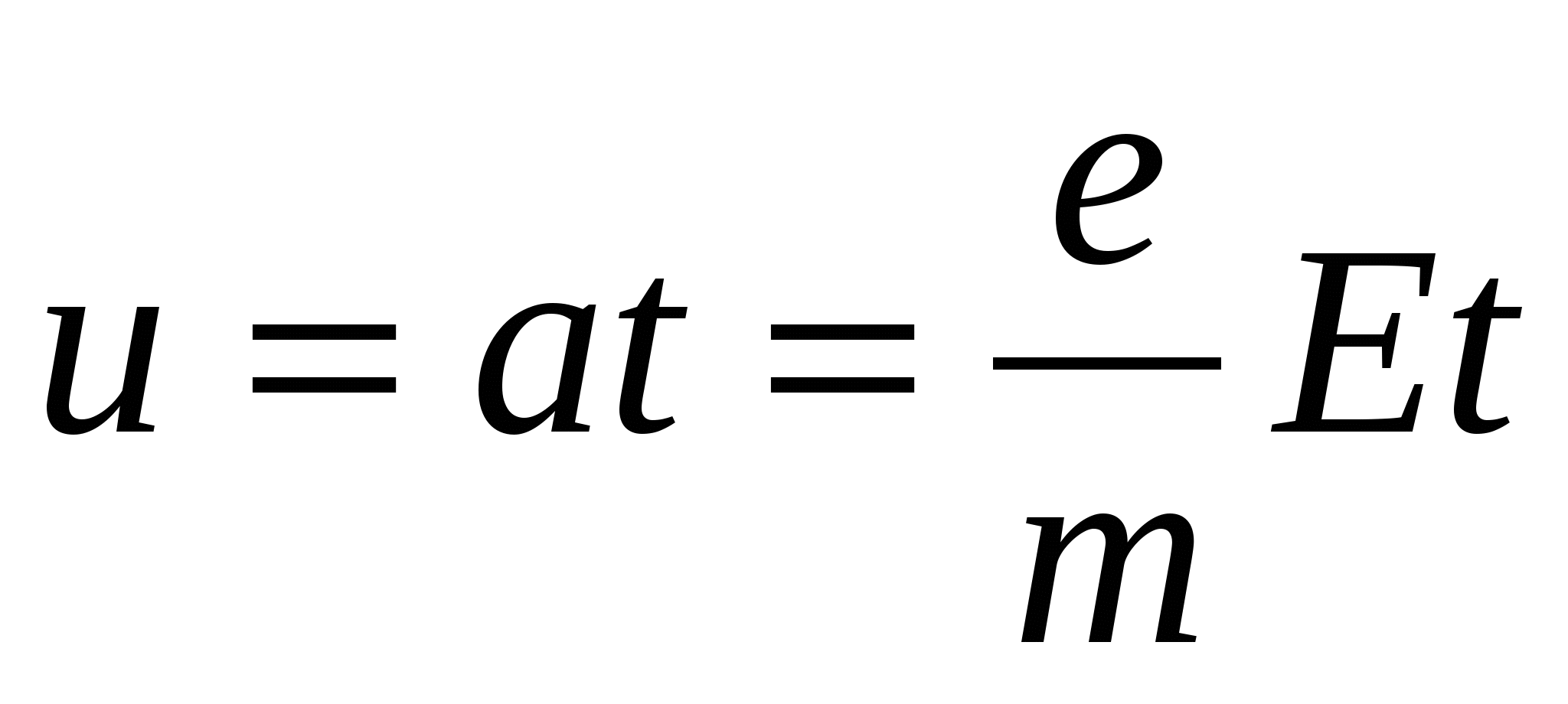 . . | (15.22) |
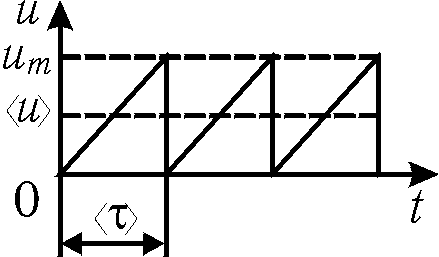
Рис. 15.4
Из формулы (15.22) следует, что скорость электрона u
с течением времени должна возрастать неограниченно. Однако через некоторый промежуток времени электрон испытывает столкновение с ионом кристаллической решетки и останавливается. Схематически зависимость скорости направленного движения от времени изображена на рис. 15.4.
Среднее время между двумя последовательными столкновениями электрона
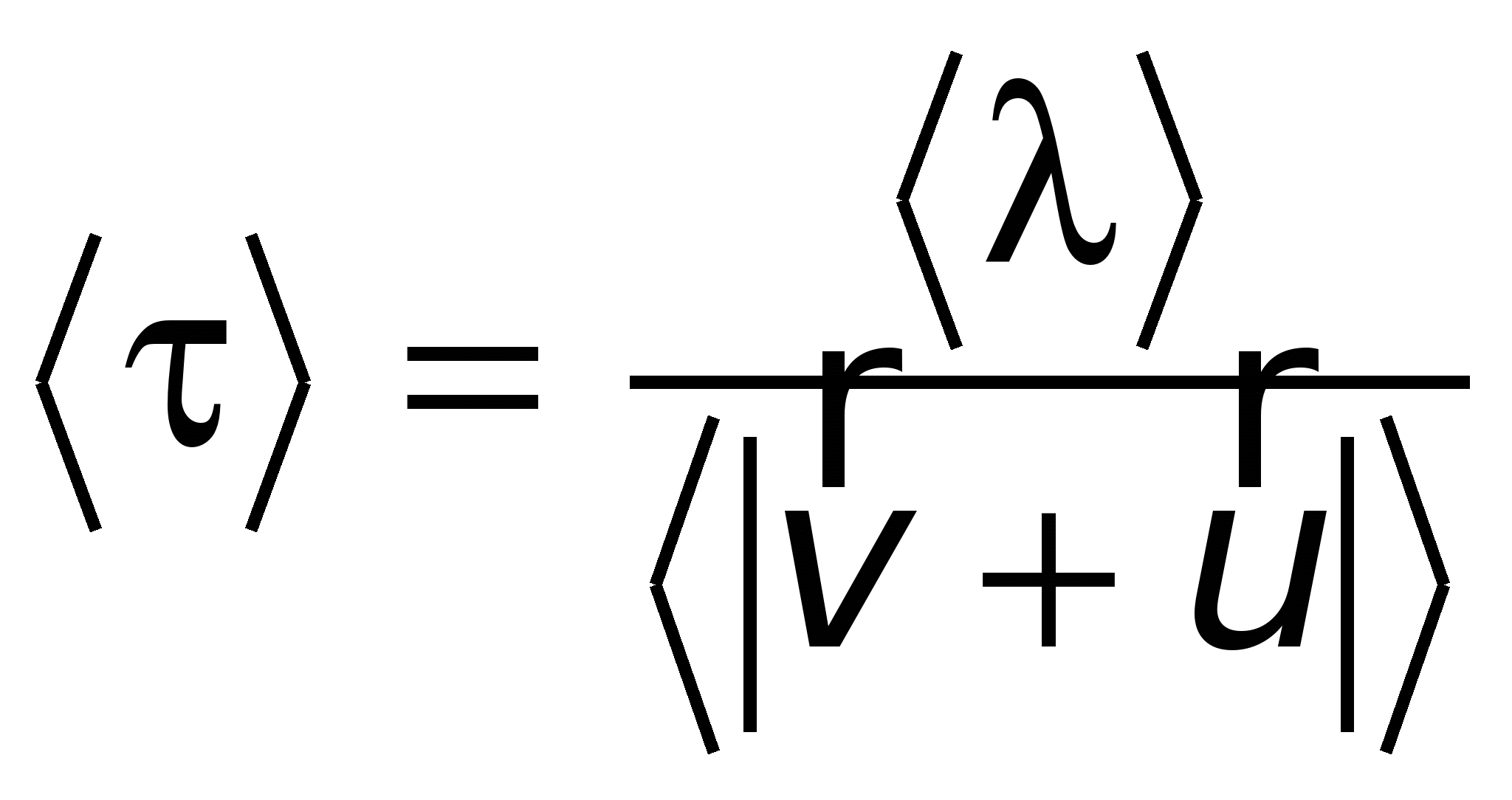 , , | (15.23) |
где
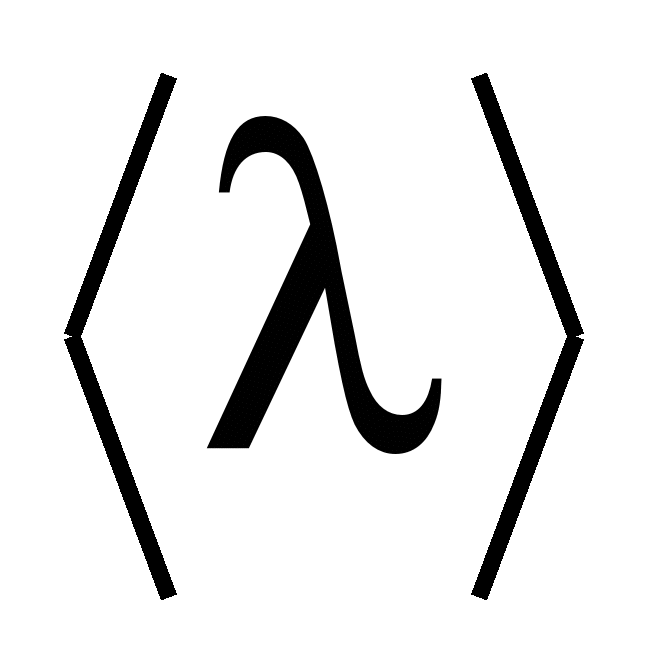 – средняя длина свободного пробега электрона;
– средняя длина свободного пробега электрона; 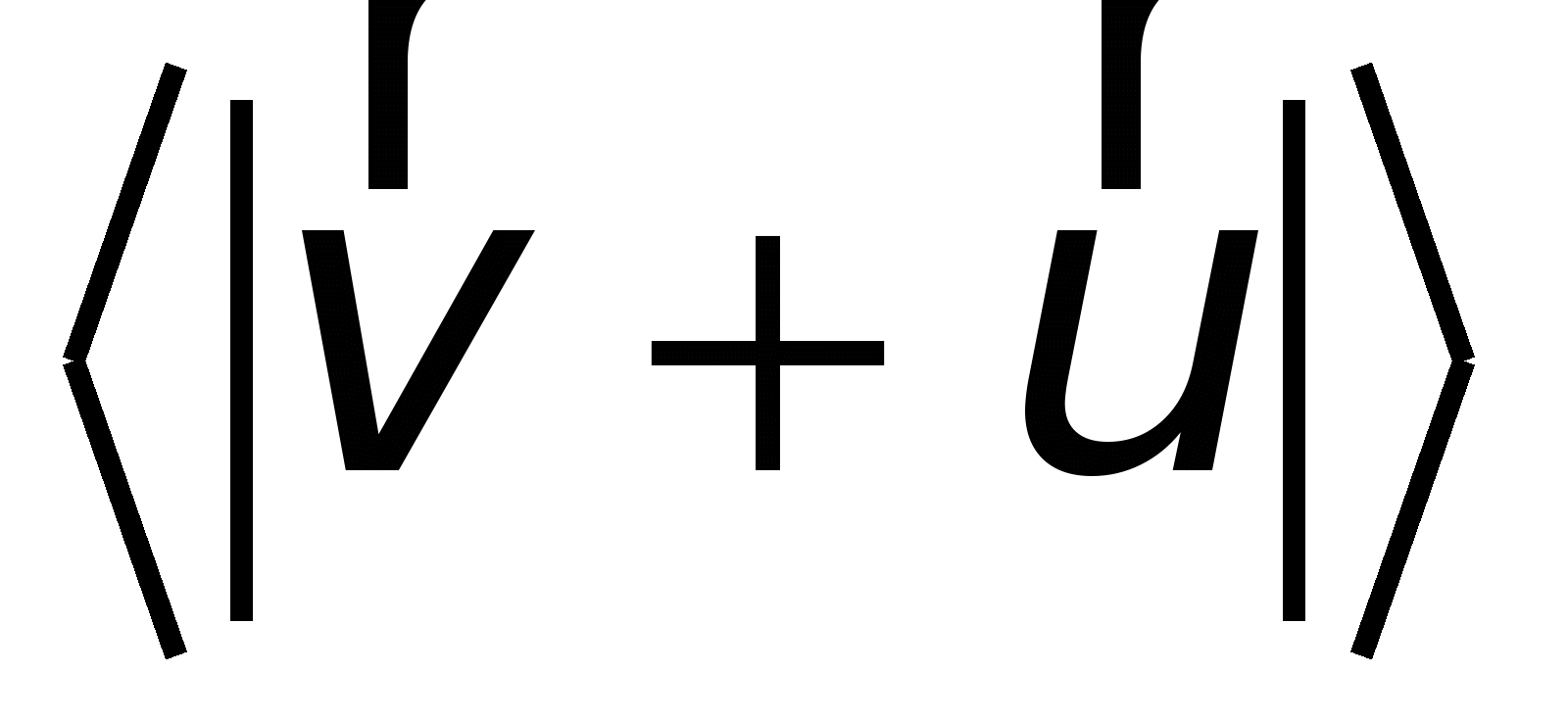 – среднее значение его скорости, которая является векторной суммой скоростей хаотического и направленного движений.
– среднее значение его скорости, которая является векторной суммой скоростей хаотического и направленного движений.В силу неравенства (15.21) скоростью направленного движения можно пренебречь, поэтому
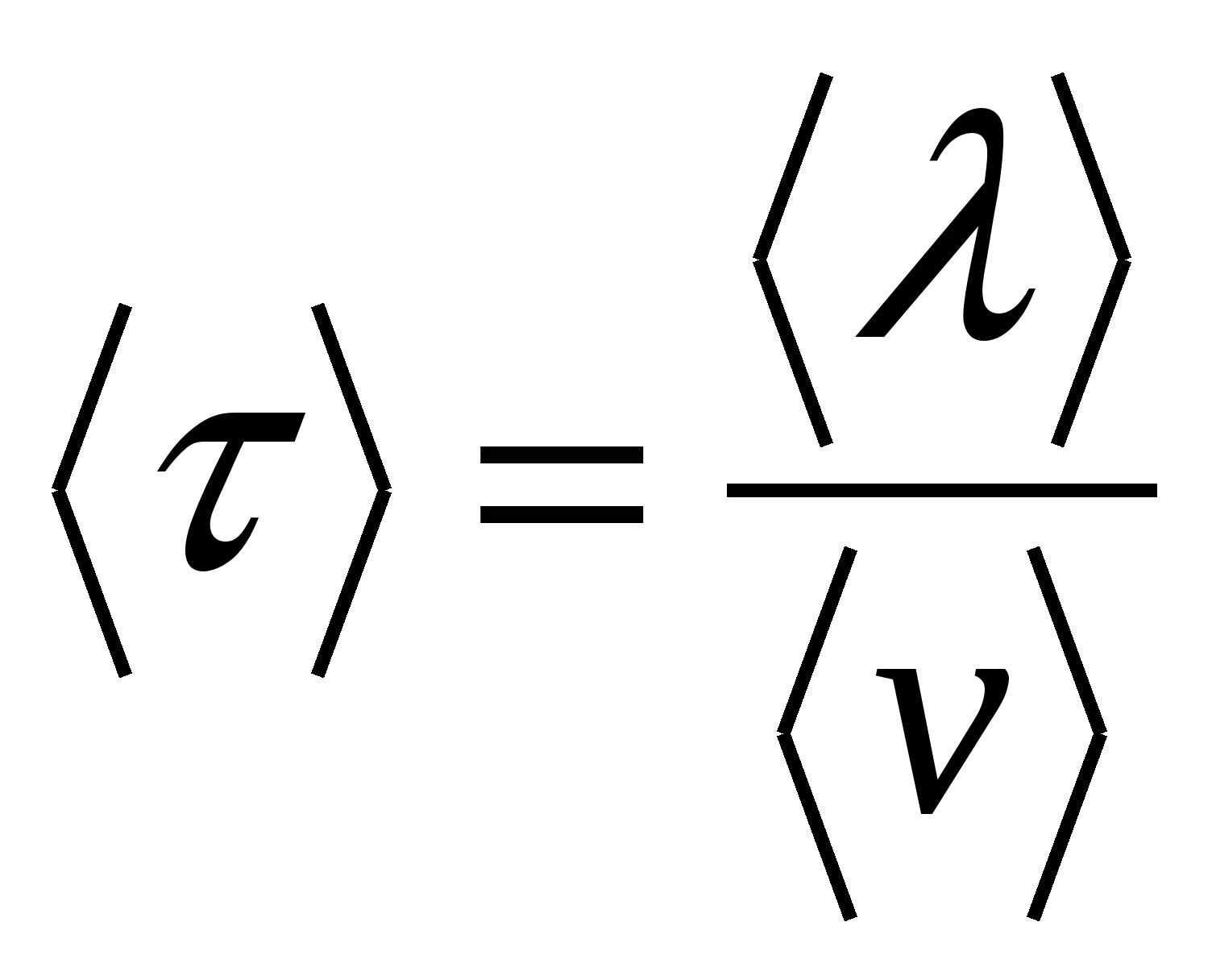 . .
через характеристики электронного газа. Исходя из представлений классической электронной теории металлов, получим теперь закон Джоуля–Ленца. К концу свободного пробега электрон обладает кинетической энергией направленного движения
Подставляя сюда значение максимальной скорости направленного движения электрона из (15.25) и учитывая, что среднее число столкновений за 1 с
получаем закон Джоуля–Ленца
Из сопоставления (15.30) и (15.20) находим такое же выражение для удельной теплопроводности, как и в законе Ома (см. (15.28)). Несмотря на очевидные успехи классической электронной теории металлов, она, тем не менее, столкнулась с рядом трудностей. В частности классическая теория неправильно предсказывает зависимость сопротивления металла от температуры. Анализ выражения (15.29) показывает, что от температуры зависит лишь скорость хаотического движения. При этом (см. формулу (8.18)) Рис. 15.5
Первое правило Кирхгофа.
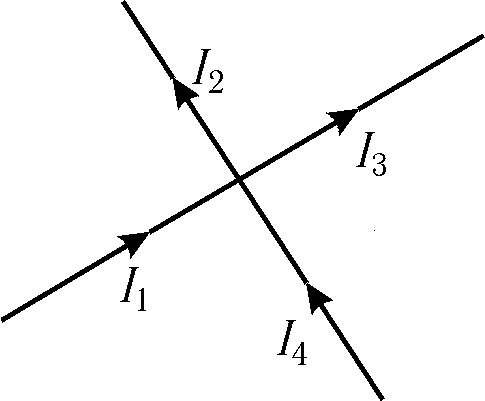
Алгебраическая сумма токов, сходящихся в узле, равна нулю, т.е.
Узлом называется точка цепи, где пересекаются три и более проводников. Ток берется со знаком "+", если он входит в узел; выходящий из узла ток берется со знаком "-". Рис. 15.6
т.е. сумма токов, входящих в узел, равна сумме токов, выходящих из него. Первое правило Кирхгофа – следствие закона сохранения электрического заряда: заряды, попав в узел, никуда не исчезают и не накапливаются. ^
Второе правило Кирхгофа.
Алгебраическая сумма падений напряжения в замкнутом контуре, выделенном из сложной цепи, равна алгебраической сумме ЭДС, включенных в этот контур:
Падение напряжения берется со знаком "+", если ток направлен в сторону обхода контура, и "-" в противном случае. ЭДС берется со знаком "+", если она действует в направлении обхода, и "-" – в противном случае. Направление обхода выбирается произвольно. Для определенности выберем направление обхода по часовой стрелке. Запишем для примера второе правило Кирхгофа для контуров ^ ABCFA и ABCDEFA (рис. 15.7): контур ABCFA : I 1 R 1 + I 2 R 2 = E 1 – E 2 ; контур ABCDEFA: I 1 R 1 - I 3 R 3 = E 1 – E 3 . В общем случае, когда в цепи имеется n узлов и m контуров, нужно составить n -1 уравнение по первому правилу Кирхгофа и m -1 уравнение по второму правилу. 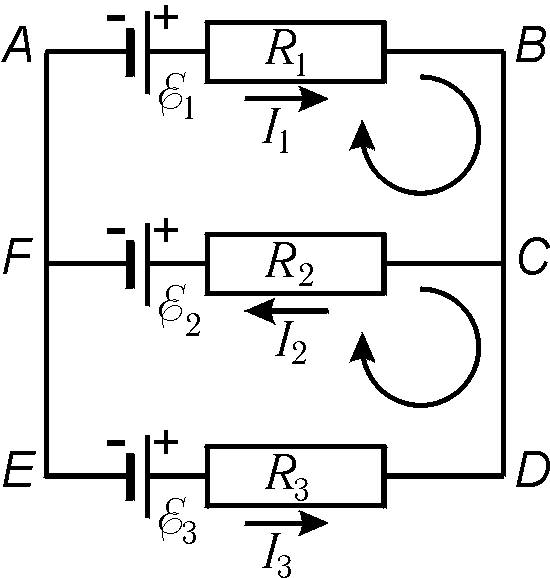 Рис. 15.7
Лекція 25. |
. Энергия системы неподвижных точечных зарядов . Как мы уже знаем, электростатические силы взаимодействия консервативны; значит, система зарядов обладает потенциальной энергией. Будем искать потенциальную энергию системы двух неподвижных точечных зарядов Q 1 и Q 2 , которые находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией (используем формулу потенциала уединенного заряда):
где φ 12 и φ 21 - соответственно потенциалы, которые создаются зарядом Q 2 в точке нахождения заряда Q 1 и зарядом Q 1 в точке нахождения заряда Q 2 . Согласно,
поэтому W 1 = W 2 = W и
Добавляя к нашей системе из двух зарядов последовательно заряды Q 3 , Q 4 , ... , можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна
![]() (1)
(1)
где φ i - потенциал, который создается в точке, где находится заряд Q i , всеми зарядами, кроме i-го.
2. Энергия заряженного уединенного проводника . Рассмотрим уединенный проводник, заряд, потенциал и емкость которого соответственно равны Q, φ и С. Увеличим заряд этого проводника на dQ. Для этого необходимо перенести заряд dQ из бесконечности на уединенный проводник, при этом затратив на это работу, которая равна
");?>" alt="элементарная работа сил электрического поля заряженного проводника">
Чтобы зарядить тело от нулевого потенциала до φ, нужно совершить работу
![]() (2)
(2)
Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:
Формулу (3) можно также получить и условия, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Если φ - потенциал проводника, то из (1) найдем
![]()
где Q=∑Q i - заряд проводника.
3. Энергия заряженного конденсатора
. Конденсатор состоит из заряженных проводников поэтому обладает энергией, которая из формулы (3) равна
(4)
где Q - заряд конденсатора, С - его емкость, Δφ - разность потенциалов между обкладками конденсатора.
Используя выражение (4), будем искать механическую (пондеромоторную) силу
, с которой пластины конденсатора притягиваются друг к другу. Для этого сделаем предположение, что расстояние х между пластинами изменилось на величину dx. Тогда действующая сила совершает работу dA=Fdx вследствие уменьшения потенциальной энергии системы Fdx = - dW, откуда
(5)
Подставив в (4) выражение для емкости плоского конденсатора, получим ![]() (6)
(6)
Продифференцировав при фиксированном значении энергии (см. (5) и (6)), получим искомую силу:
![]()
где знак минус указывает, что сила F является силой притяжения.
4. Энергия электростатического поля . Используем выражение (4), которое выражает энергию плоского конденсатора посредством зарядов и потенциалов, и спользуя выражением для емкости плоского конденсатора (C=ε 0 εS/d) и разности потенциалов между его обкладками (Δφ=Ed. Тогда
где V= Sd - объем конденсатора. Формула (7) говорит о том, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, - напряженность Е.
Объемная плотность энергии электростатического поля (энергия единицы объема)
Выражение (8) справедливо только для изотропного диэлектрика, для которого выполняется соотношение: Р = æε 0 Е .
Формулы (4) и (7) соответственно выражают энергию конденсатора через заряд на его обкладках и через напряженность поля. Возникает вопрос о локализации электростатической энергии и что является ее носителем - заряды или поле? Ответ на этот вопрос может дать только опыт. Электростатика занимается изучением постоянных во времени поля неподвижных зарядов, т. е. в ней поля и попродившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на данный вопрос не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать отдельно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, которые способны переносить энергию. Это убедительно подтверждает основное положение теории близкодействия о том, что энергия локализована в поле и что носителем энергии является поле .
Энергию плоского конденсатора можно вычислить, считая, что одна обкладка его создает поле, а вторая в нем находится.
Пусть отрицательно заряженная обкладка имеет потенциал равный нулю. Тогда потенциал положительно заряженной ![]() .
.
![]() .
.
![]()
Энергию заряженного конденсатора можно считать локализованной между его обкладками, если расстояние между ними мало по сравнению с размерами обкладок. Значит, энергия электростатического поля практически не рассеивается и его можно считать сосредоточенным в объеме и однородным. Объемной плотностью энергии называют энергию, приходящуюся в однородном электростатическом поле на единицу объема.
Для плоского конденсатора ![]() =>
=>
Т.е. плотность энергии однородного электростатического поля пропорциональна квадрату его напряженности. Такой же вывод можно сделать и для микрообластей неоднородного поля. Формула (*) позволяет говорить о поле как об объекте, реально существующем, т.к. у этого объекта есть плотность энергии.

ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОН ОМА ДЛЯ ОДНОРОДНОГО УЧАСТКА ЦЕПИ.
Отличительной особенностью проводников является наличие в них свободных электрических зарядов. При отсутствии электрического поля свободные заряды в проводниках перемещаются хаотично. Если на концах проводника создать и поддерживать разность потенциалов, то в нем возникнет однородное электростатическое поле. Свободные заряды, кроме беспорядочного, приобретут упорядоченное движение. В проводнике возникнет электрический ток. ЭЛЕКТРИЧЕСКИМ ТОКОМ называется упорядоченное движение нескомпенсированного электрического заряда. За направление тока принимается направление движения положительных зарядов (против отрицательных). Мерой электрического тока является СИЛА ТОКА - ЭЛЕКТРИЧЕСКИЙ ЗАРЯД, ПРОХОДЯЩИЙ ЧЕРЕЗ ПОПЕРЕЧНОЕ СЕЧЕНИЕ ПРОВОДНИКА В ЕДИНИЦУ ВРЕМЕНИ.
О существовании тока можно судить по его действиям.
Существуют:
а) Тепловое действие. Проводники при прохождении по ним электрического тока нагреваются. Тепловое действие отсутствует в сверхпроводниках.
б) Световое действие. Ток, проходя по газам, может заставить их светиться.
в) Химическое действие. Ток, проходя по растворам солей, кислот, щелочей, вызывает выделение веществ на электродах.
г) Магнитное действие. Провода с током взаимодействуют через магнитное поле.
д) Физиологическое действие. Ток, проходя по мышцам, вызывает их сокращение.
Магнитное взаимодействие проводников с током дало возможность ввести единицу силы тока - ампер, являющуюся основной единицей в СИ.
Ампер - это сила тока, который при прохождении по двум параллельным, бесконечно длинным проводникам, находящимся в вакууме на расстоянии 1м друг от друга, вызывает силу взаимодействия между ними в 2×1O -7 Н на каждый метр длины.
Силу тока легко выразить через параметры создающих его свободных зарядов. Пусть концентрация свободных частиц, каждая из которых несет заряд q 0 , в проводнике сечения S равна n, а скорость их поступательного движения равна v. Тогда за время t через поперечное сечение проводника пройдет частиц, которые перенесут заряд . Сила тока при этом будет:
Легко убедиться в том, что скорость частиц в проводнике с током мала. Со скоростью света в нем распространяется электрическое поле.
Векторной величиной, характеризующей электрический ток, является плотность тока - отношение силы тока, идущего по проводнику, к его площади.
Плотность тока направлена по напряженности поля в проводнике.
Исследуя зависимость силы тока от разности потенциалов на концах участка цепи, Ом экспериментально установил, что СИЛА ТОКА В УЧАСТКЕ ЦЕПИ ПРЯМО ПРОПОРЦИОНАЛЬНА РАЗНОСТИ ПОТЕНЦИАЛОВ НА КОНЦАХ УЧАСТКА И ОБРАТНО ПРОПОРЦИОНАЛЬНА ЕГО СОПРОТИВЛЕНИЮ . В этом состоит закон Ома для однородного участка цепи.
Сопротивление участка цепи равно 1Ом, если при разности потенциалов на его концах в 1В сила тока в нем 1А. Сопротивление проводника объясняется взаимодействием движущихся свободных заряженных частиц, с атомами или ионами, совершающими тепловое движение около своих положений равновесия, потерей ими при этом скорости и части кинетической энергии. Сопротивление проводника зависит от его материала, длины, сечения и температуры. Экспериментально установлено:
где L - длина проводника, S - площадь его поперечного сечения,
r - удельное сопротивление проводника, т.е. сопротивление куба из данного проводника с ребром в 1м, если ток идет вдоль нормали к двум противоположным его граням. .
Экспериментально найдена зависимость электрического сопротивления от температуры.
где R 0 - сопротивление проводника при О 0 C, R - сопротивление при t 0 С, a - температурный коэффициент сопротивления, равный относительному изменению сопротивления проводника при нагревании от О до 1 0 C.
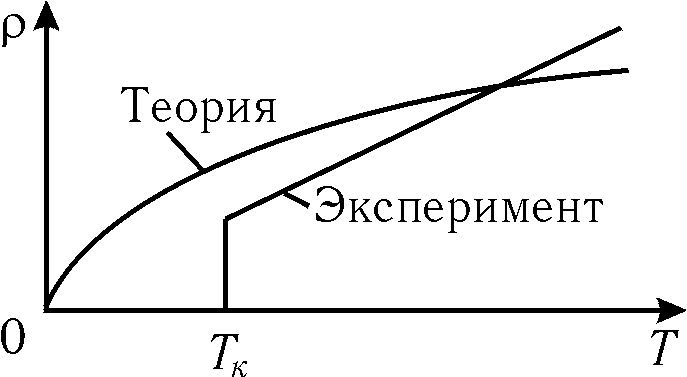
Для металлов a>О, т.е. при нагревании сопротивление металла увеличивается. Классическая физика не может дать точного математического описания зависимости сопротивления металлов от температуры. В квантовой физике доказано, что время свободного пробега электронов в металле обратно пропорционально его абсолютной температуре (исключая абсолютный нуль температуры), а это ведет к возрастанию сопротивления при нагревании. Для растворов электролитов и газов a<О, т.е. при нагревании их сопротивление уменьшается. Это объясняется тем, что при нагревании растворов электролитов и газов в них образуется больше носителей свободных зарядов.
При очень низких температурах (для свинца 7,2 К) сопротивление проводника резко падает до нуля. Это явление называется сверхпроводимостью. Оно нашло широкое практическое применение для создания сверхмощных электромагнитов, ЭВМ, приборов и т.д. В настоящее время найдены соединения, переходящие в сверхпроводящее состояние при температурах порядка 1ООК. Объяснение явления сверхпроводимости дает только квантовая физика.
Опыт Рике: по цепи из медных и алюминиевых цилиндров, плотно подогнанных друг к другу, больше года пропускался электрический ток. При этом прошел заряд 3×1О 6 Кл. Анализ места соприкосновения цилиндров не обнаружил даже следов проникновения одного металла в другой. Т.е. Прохождение тока через металлы не сопровождается их химическим изменением. Это говорит о том, что атомы металла в проводнике с током не перемещаются.
По электронной теории отрицательные заряды атомов металлов - валентные электроны, сравнительно легко могут быть отделены от атома. Атом при этом образует положительный ион. В металле всегда есть значительное количество свободных электронов. Эти электроны под действием электрического поля легко перемещаются по металлу. Ионы же составляют остов металла, образуя кристаллическую решетку. Явление фотоэффекта показывает, что электроны легко могут быть вырваны из металла, тогда как положительные заряды крепко связаны с кристаллической решеткой металла. Непосредственным подтверждением того, что носителями электрического тока в металлах являются свободные электроны стали опыты Мандельштама и Папалекси (1912) и Толмена и Стюарта (1916 г). При резкой остановке быстро вращающейся катушки из проводника, соединенной с гальванометром, свободные электроны, вследствие инертности, некоторое время продолжают движение, создавая ток в цепи. Направление тока показывает знак заряда. Определение удельного заряда частиц, т.е. отношения заряда частиц к их массе, убедительно показало, что движутся электроны. Итак, электрический ток в металле - это направленное движение свободных электронов.
Электронная теория проводимости, давая правильные качественные выводы, не может дать точное количественное описание многих экспериментальных соотношений, полное описание которых возможно только в квантовой физике.
1. Энергия системы точечных неподвижных зарядов . Электростатические силы консервативны и система зарядов обладает потенциальной энергией. Пусть заряды Q 1 и Q 2 находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией
где φ 12 и φ 21 – соответственно потенциалы, создаваемые зарядом Q 2 в точке нахождения заряда Q 1 , и наоборот.
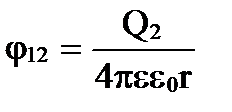 ;
; 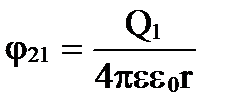 .
.
W 1 = W 2 =W = Q 1 φ 12 = Q 2 φ 21 = ½ (Q 1 φ 12 + Q 2 φ 21).
Добавляя к системе из двух зарядов последовательно заряды Q 3 , Q 4 , …, Q n , можно убедиться, что энергия взаимодействия системы зарядов равна
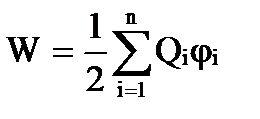 ,
,
где φ i – потенциал, создаваемый в той точке, где находится заряд Q i , всеми зарядами, кроме i-го.
2. Энергия заряженного уединенного проводника . Пусть имеется уединенный проводник, заряд, емкость и потенциал которого Q, C, φ.
Увеличим заряд на dQ. Для этого необходимо перенести заряд dQ из бесконечности к поверхности проводника, затратив на это работу, равную
dA = φdQ = C φd φ
Чтобы зарядить тело от нулевого потенциала до потенциала равного φ необходимо совершить работу
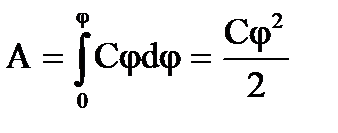
Энергия заряженного проводника будет равна этой работе
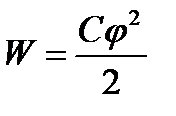
Учитывая, что 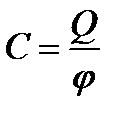 , эту энергию можно представить в виде
, эту энергию можно представить в виде
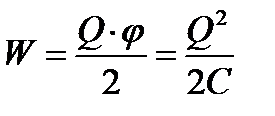
3. Энергия заряженного конденсатора . Как всякий заряженный проводник, конденсатор обладает энергией
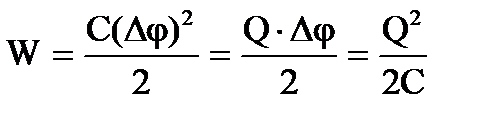
где Q - заряд конденсатора, С – его емкость и Δφ – разность потенциалов между обкладками.
Используя выражение для энергии, можно найти механическую (пондеромоторную) силу, с которой пластины конденсатора притягивают друг друга. Для этого предположим, что расстояние х между пластинами меняется на величину dx. Тогда действующая сила совершает работу равную
за счет уменьшения потенциальной энергии Fdx = - dW, откуда
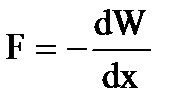 .
.
Подставляя в формулу энергии 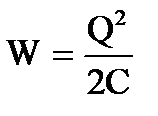 выражение емкости
выражение емкости
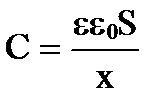 , получим
, получим
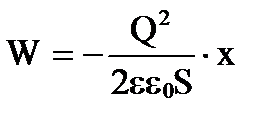 .
.
Дифференцируя W по х , найдем силу F
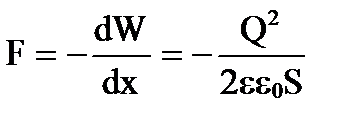 ,
,
где знак “минус“ указывает, что сила F стремится уменьшить расстояние между пластинами, т.е. является силой притяжения. Подставляя выражение плотности зарядов на пластинках 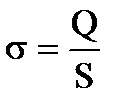 , получим
, получим 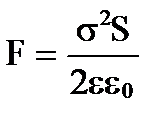 .
.
Учитывая напряжённость поля, что Е = 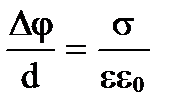 , получим
, получим
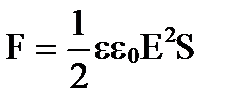 .
.
Давление на пластины диэлектрика, помещенные в зазоре конденсатора, будет
![]()
4. Энергия электростатического поля
.
Преобразуем формулу энергии плоского конденсатора 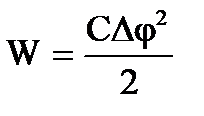 , используя формулы
, используя формулы
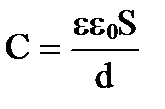 и Δφ = Еd.
и Δφ = Еd.
Получим ,
где V – объем пространства между пластинами конденсатора, в котором сосредоточена энергия его поля W.
Объемную плотность энергии поля w – это энергия, заключённая в единице объёма электрического поля и она равна
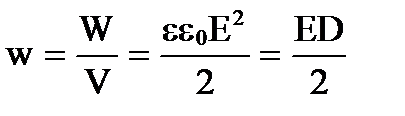 .
.
Единица измерения [Дж/м 3 ].
Видно, что объемная плотность энергии поля зависит только от характеристик поля и среды.

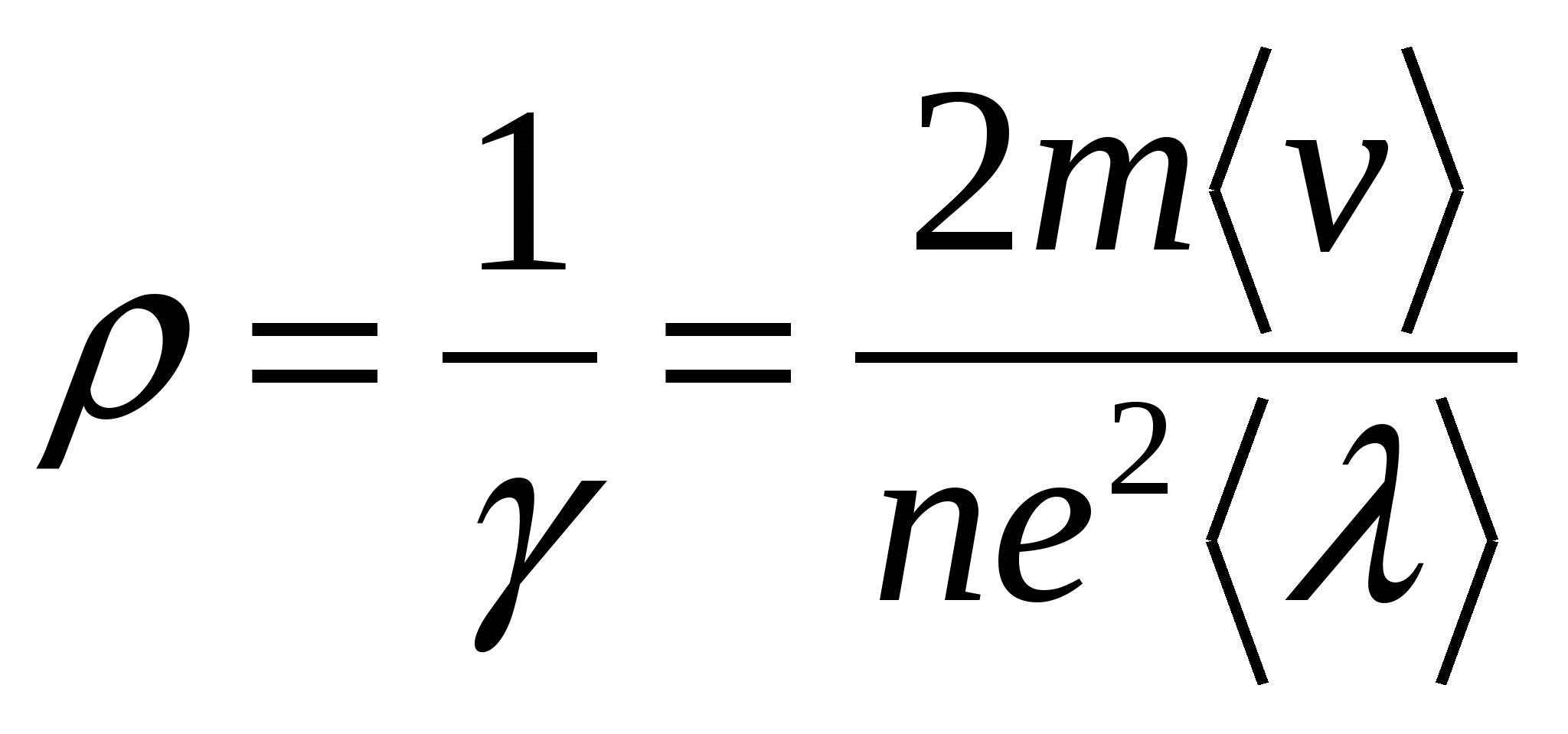 .
.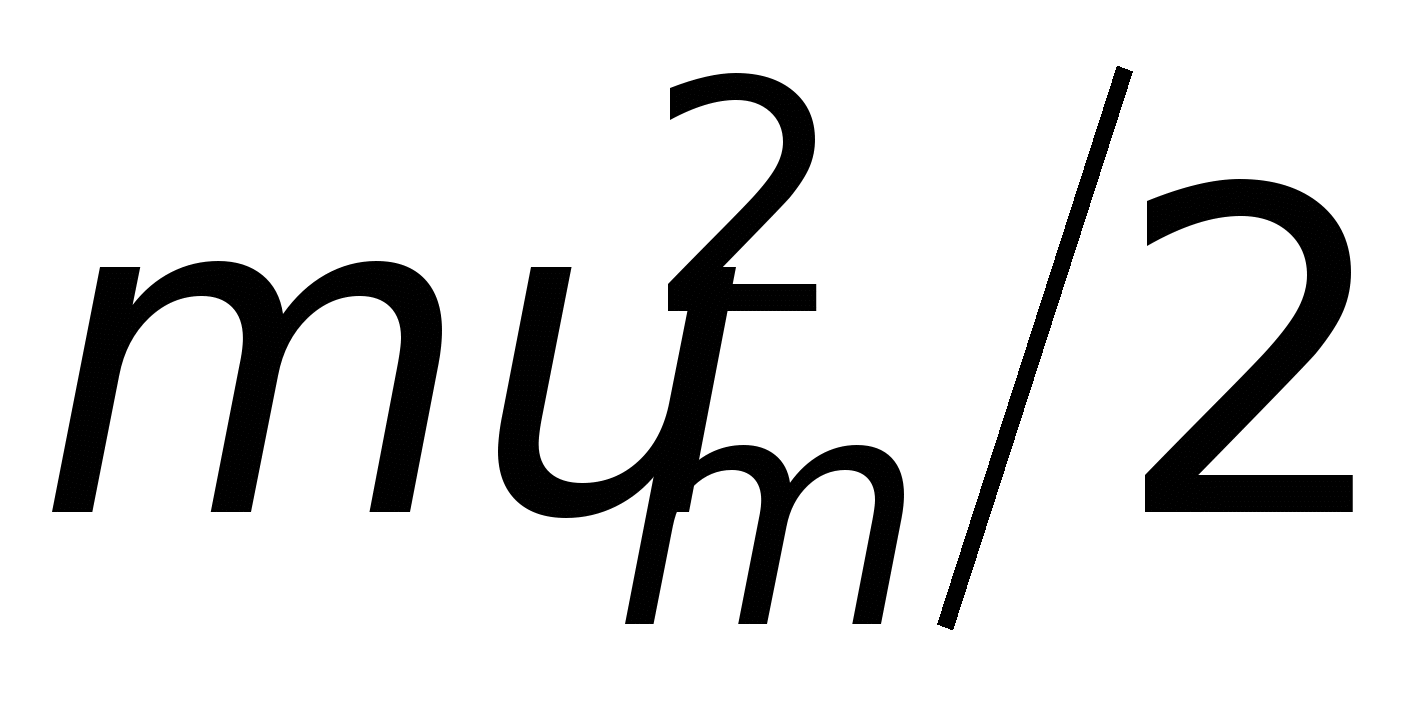 . Эту энергию электрон полностью передает иону кристаллической решетки при столкновении с ним. Множество таких столкновений приводит к выделению джоулевой теплоты. Если концентрация электронов n
, и каждый из них сталкивается
. Эту энергию электрон полностью передает иону кристаллической решетки при столкновении с ним. Множество таких столкновений приводит к выделению джоулевой теплоты. Если концентрация электронов n
, и каждый из них сталкивается  раз за 1 с, то в единичном объеме проводника выделиться мощность
раз за 1 с, то в единичном объеме проводника выделиться мощность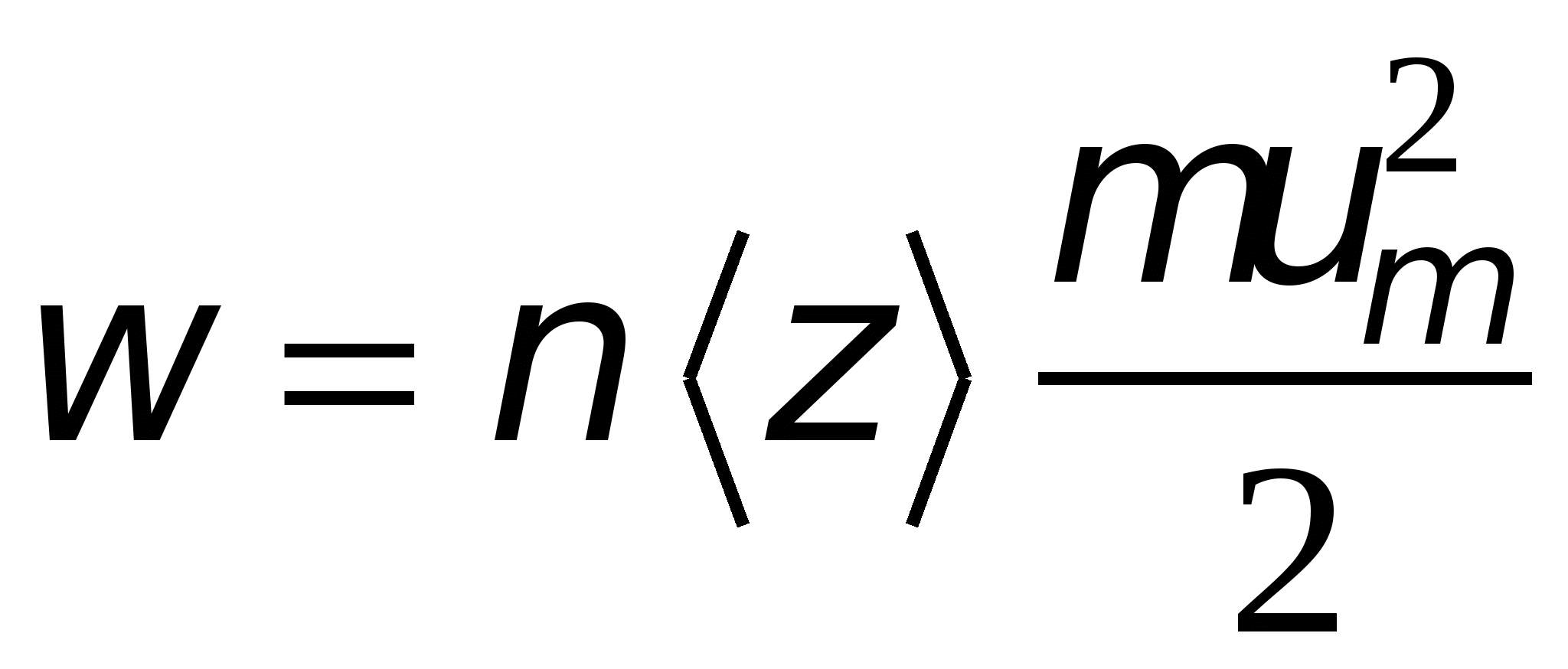 .
.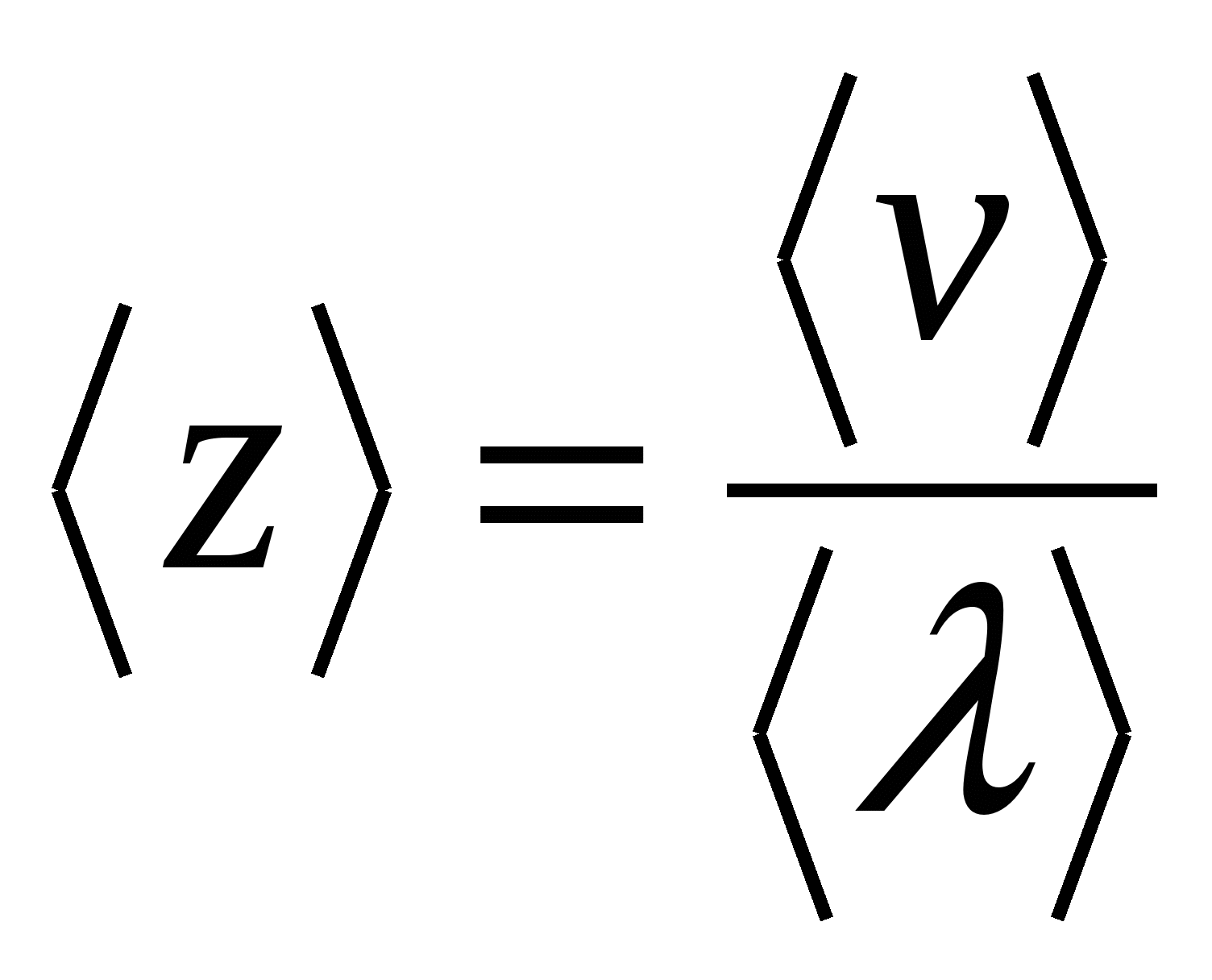 ,
, 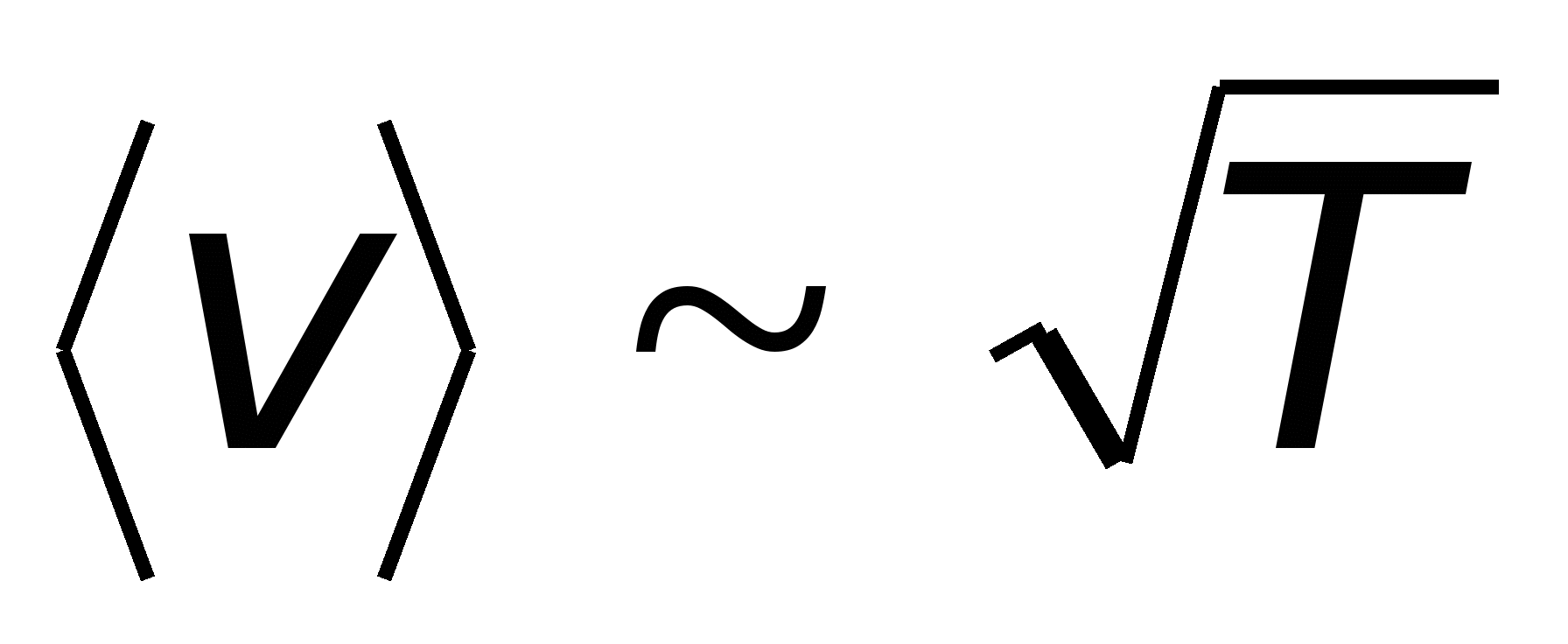 , следовательно, удельное сопротивление
, следовательно, удельное сопротивление 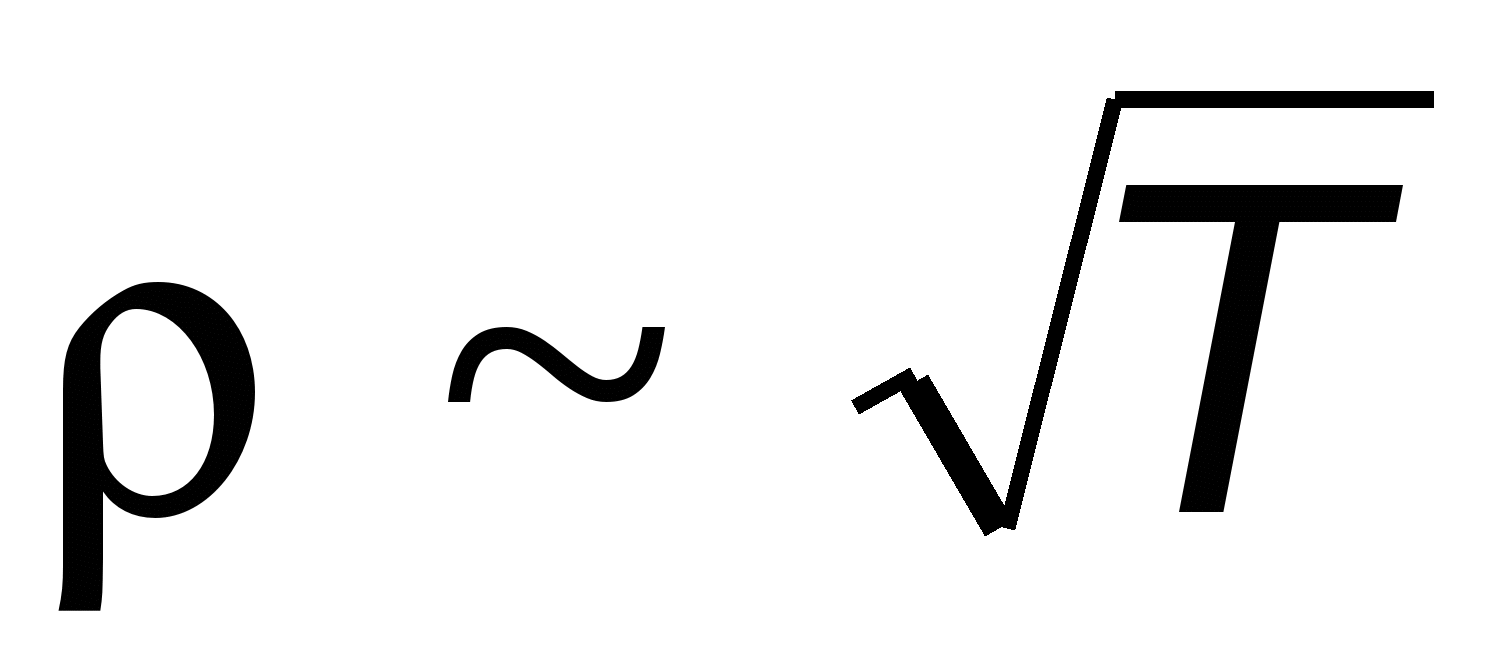 . Между тем опыт показывает, что линейно зависит от температуры
. Между тем опыт показывает, что линейно зависит от температуры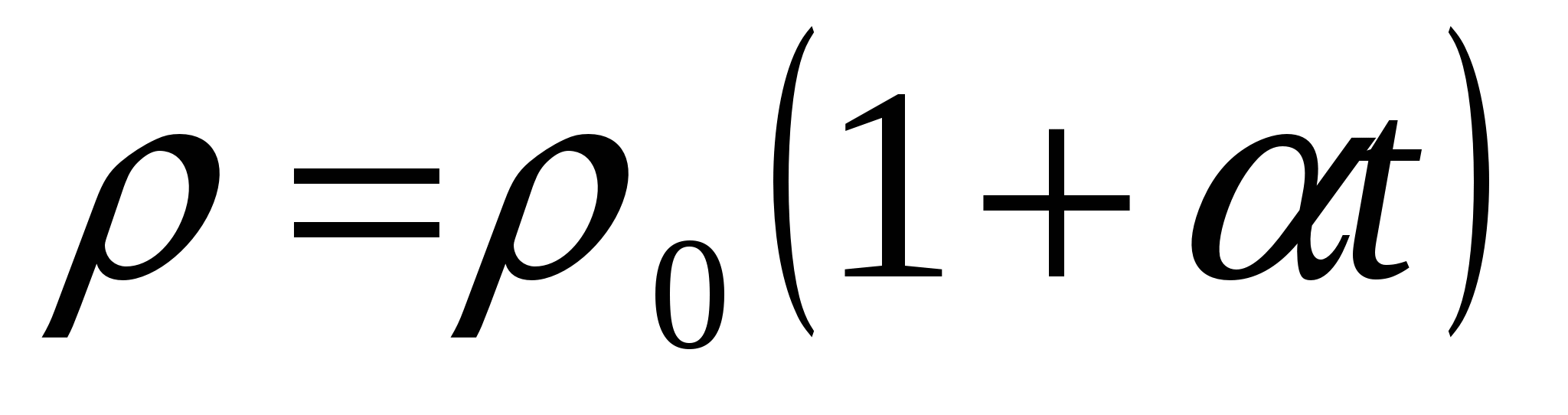 ,
,
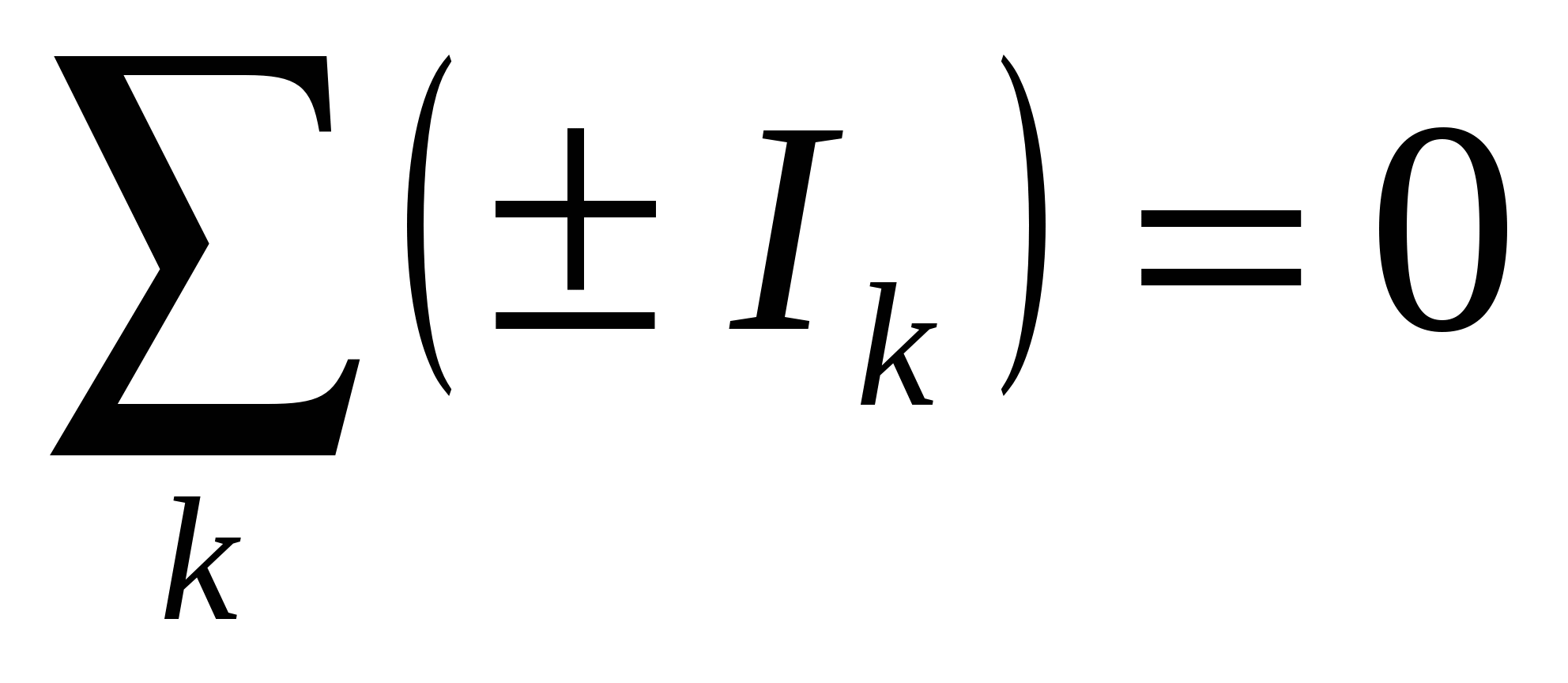 .
.
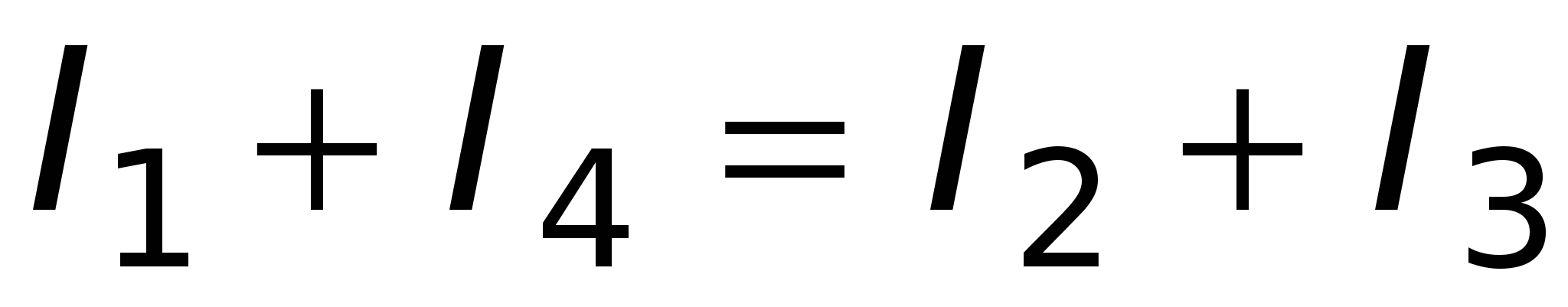 ,
,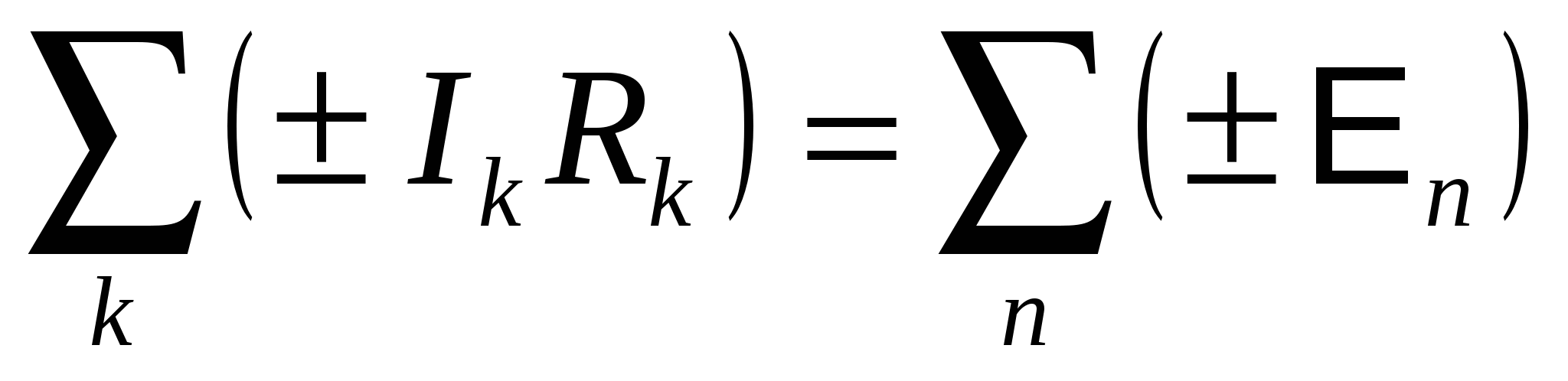 .
.